基于位移的钢框架结构可靠度研究
王凯 颜庆智 王中辉 刘作勋
摘要:
石化结构经常因其设备管线复杂的布置而造成结构的刚度分布不均匀,设计经常会过于保守。为了对基于位移的钢框架结构可靠度进行研究,利用有限元软件对炼化平台钢框架结构进行建模、计算、分析,在PDS(概率设计系统)模块中运用Monte Carlo法对结构位移的可靠度进行分析,获取炼化平台钢框架结构的最大位移与随机输入变量之间关系的计算结果。该结果表明该炼化平台钢框架结构的设计比较保守,造成了钢材的浪费。为了实现结构设计的经济性,应根据计算得到的灵敏度图,在满足结构可靠性的基础上,将图中非敏感性因子的截面尺寸进行优化再设计,得出安全经济的设计方案,为以后石油化工行业钢框架结构的设计提供参考。
关键词:
钢框架;结构位移;Monte Carlo;可靠度
中图分类号:TU 391文献标识码:A文章编号:1001-005X(2018)01-0091-06
Abstract:
Petrochemical structures are often characterized by uneven distribution of stiffness due to the complicated arrangement of its equipment pipelines,and designs are often overly conservative.In order to analysis of the steel frame structure based on displacement,the finite element software was used to model,calculate and analyze the steel frame structure of refining platform.In the PDS(the probability design system)module,the Monte Carlo method was used to analyze the reliability of structural displacement in the PDS module to obtain the calculation results of the relationship between the maximum displacement and the random input variables of the steel frame structure of the refining platform.The results revealed that the section size of the steel frame structure was more conservative,resulting in the waste of steel.In order to realize the design of the structures economy,we should optimize and redesign the crosssectional dimensions of nonsensitive factors in the graph based on the calculated sensitivity diagram to meet the structural reliability,and draw a safe and economical design plan for the future petrochemical industry,which could provide reference for the future design of steel frame structure in petrochemical industry.
Keywords:
steel frame structure;displacement;Monte Carlo;reliability
0引言
鋼结构在石油化工领域中应用非常广泛,石化产业的炼化平台钢框架结构因其生产设备与生产工艺上的要求,而具有自己独特的特点。石化设备大多是露天或敞开式布置,由于生产工艺的要求,管线的布置往往是纵横交错的,数量多而且质量以及尺寸都很大,因而造成结构的刚度和质量分布不均;大多数的石化设备以及管线的布置是不均匀的,造成了结构受力的复杂,设计方法也同钢结构设计规范有所差异,进行结构设计时,设计经常会过于保守,而且对于钢框架平台的研究较少,因此,需要对炼化平台钢框架结构进行优化分析[1]。
1蒙托卡罗法
结构体系可靠度的计算方法大致包括:失效模式法、Monte Carlo法、响应面法和随机有限元法等。Monte Carlo法[2-3]不受功能函数非线性的影响,可以通过多次模拟试验就可以得到比较精确的结果。Monte Carlo法又称为概率统计模拟方法,该方法是按随机抽样规律方法产生子样本,而后进行子样本的统计分析,分析解出问题的值。在ANSYS可靠度数值分析模块中Monte Carlo法的抽样方法包括直接抽样法与拉丁超立方抽样方法,也可以自定义抽样类型,拉丁超立方抽样方法[4]其基本思路是把随机变量的采样区域通过细分为等概率空间将样本均匀分布在整个问题域中,并在每个段中绘制一个样本。拉丁超立方抽样方法[5-6]可以实现样本数量的减少,而且拉丁超立方体抽样方法对于估计随机结构中的平均值与方差非常有效,而且抽样效率比单纯的Monte Carlo抽样效率略高。本文采用的是Monte Carlo法的拉丁超立方抽样法对炼化平台空间钢框架进行可靠度分析。
2基于ANSYS及Monte Carlo数值模拟
2.1工程实例
本工程项目名称为1.60 Mt/a DCC生产烯烃项目,建设地点位于山东垦利。建筑工程等级为一级;耐火等级为二级。结构类型为多层钢框架结构;建筑层数为地上三层;建筑总高度为22.495 m。设计使用年限为50 a。抗震类别为丙类,抗震设防烈度为 7度,设计基本地震加速度值为 0.10 g,钢框架结构在多遇地震荷载作用下的阻尼比采用0.04。材料采用Q235钢,这里给出结构二层平面布置,其它结构层除设备梁的截面不同外布置均相同,结构平面布置如图1所示。
该建筑结构形式为轻型钢框架结构,长度63 m,其柱距为7 m,跨度4.35 m,该石油炼化平台为多层框架结构,其中楼面材料采用5 mm厚花纹钢板。结构共两跨,柱与柱之间采用支撑连接,设备梁与框架梁间采用简支连接。在计算地震荷载作用于结构时,其正常运行时重力荷载代表值应取永久荷载与可变重力荷载组合值之和,平台活荷载为安装检修与正常生产之和取14 kN/m2,活荷载组合系数采用0.5,永久荷载的组合系数采用1.0[7]。
材料数据:
弹性模量E=2.1×1011Pa,泊松比μ=0.3,质量密度为7 850 kg/m3。
2.3ANSYS建立模型的分析步骤:
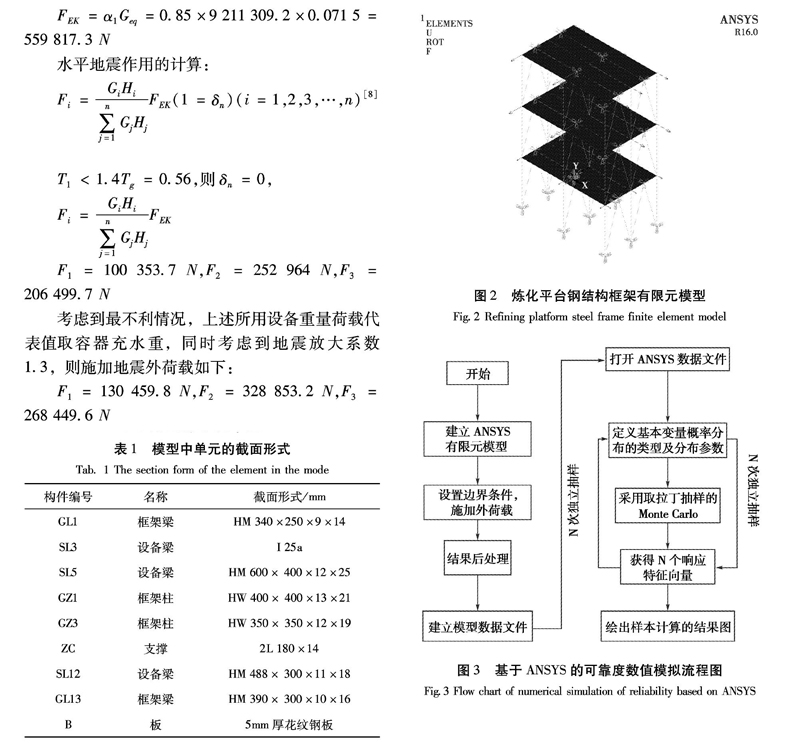
对工程实例运用ANSYS对炼化平台钢框架结构进行建模计算[9-11]。与其它钢框架结构不同,直接或者间接支承石化设备的设备梁是结构抗震的第一道防线,设备梁的抗震性能直接影响抗震设计的成败,因此,简化模型计算时,省略对平台板加劲肋的建模,同时,选取了钢框架结构中具有代表性的三榀框架进行建模计算,钢框架结构建模选用的单元类型如下:
梁柱单元采用Beam188单元;板單元选用Shell181单元;支撑杆采用Link180单元。
钢框架结构建模选用的单元的截面形式见表1。
钢框架结构建模选用单元的边界条件为:柱底边界条件为全约束,设备梁约束为X、Y、Z方向自由度,建立的模型如图2所示。
ANSYS分析步骤:首先建立几何模型、选择单元类型、设置材料数据、对几何模型赋予属性。施加位移边界条件,施加模型荷载,进行计算,进入ANSYS的PDS可靠度分析模块对模型进行模拟分析计算,模拟步骤如图3所示。
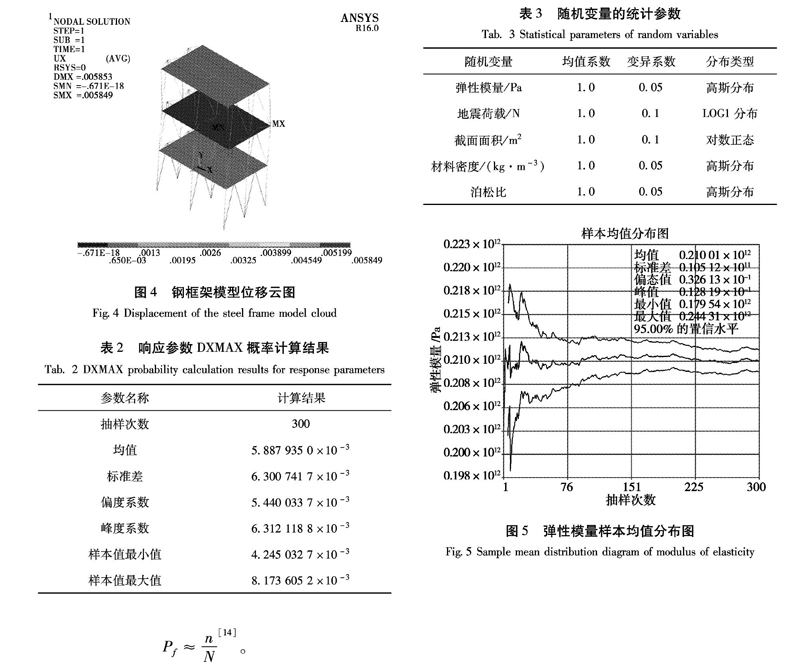
模型计算结果如图4所示。
在石油化工钢结构冷换框架设计规范中结构在地震荷载作用下的结构变形验算为层位移与层高之比不宜大于1/250[12]。地震作用下结构的位移限值为:
7 500×1/250=30 mm
由图4结构位移云图可以看出结构的最大位移在第二层,最大位移约为5.85 mm,由表 2 ANSYS模型计算结果得置信区间为[0.984 556,0.999 540],置信水平为95%条件下的DXMAX小于8×10-3的概率值为99.599%,该位移远小于30 mm。
2.4结构可靠度分析
结构的可靠性分析一般是通过概率模型来估算失效概率以此来估算可靠度的,而可靠性分析方法的主要目标就是近似的估算失效概率Pf[13],失效概率估计:
其中,N是模拟总数,n表示系统失败的模拟次数。采用Monte Carlo法对于复杂的工程问题计算是比较容易的,因此,概率设计过程中采用蒙特卡罗模拟方法进行概率设计。在利用ANSYS进行数值模拟时,可靠度分析部分定义的输出变量分别为DXMAX、DZMAX(X、Z两个方向的最大位移),对数据的抽样方法采取拉丁超立方抽样方法进行仿真计算,设置仿真循环次数为300次,假定地震荷载、钢结构的构件截面面积分布服从对数正态分布,弹性模量、材料密度、泊松比服从高斯正态分布[15-17]。具体输入变量的参数见表3。
2.5数值模拟结果分析
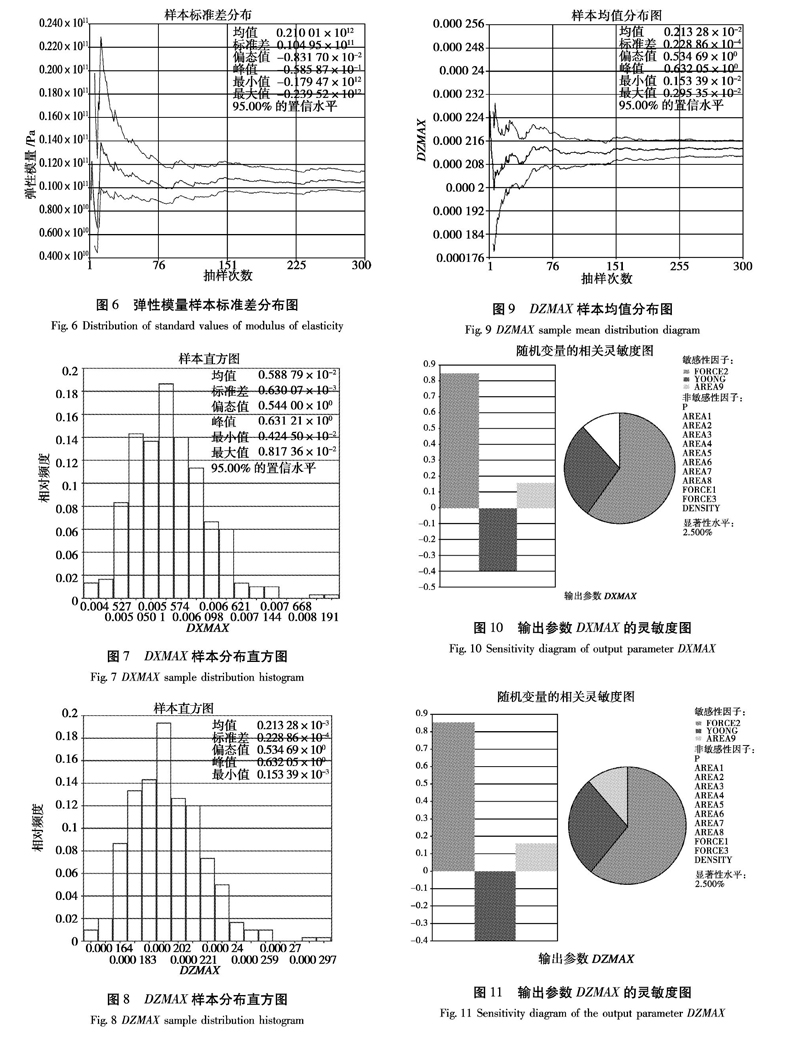
由图5、6随机变量输入的样本均值分布图、样本标准差分布图可知样本的抽样次数足够,均值、标准差均收敛,可以满足结构可靠度计算的水平。
由图7、8位移样本值的直方图可以看出在地震荷载作用下,空间框架结构的X、Z向最大位移样本值的概率分布服从极值Ⅰ型分布。
由图9可以看出该炼化平台框架在Z向的最大位为0.21 328 mm,Z向位移非常小,该石油炼化平台钢框架结构为框架-支撑体系,柱间支撑限制了结构Z向的位移,结构的最大位移出现在结构的X方向,只需分析结构X向位移即可。
在结构优化方面,经常会权衡结构的经济性、适用性,以及其它影响结构性能的因素,因此,在进行可靠度分析时,研究各个因素对结构失效的影响大小对于结构的优化具有重要意义[18]。在输入的随机变量中,确定性输入变量和参数变量都称为输入参数。灵敏度是分析结构可靠性的度量,这些输入参数的变化对于简单地评估结构的可靠性变化以及对已定的结构设计变更具有很重要的作用。灵敏度分析就是结合优化程序使用迭代方法,对结构进行优化再设计分析以使设计的总成本最小[19]。
图10、11柱状图是根据灵敏度大小从左到右依次排列,可以看出作用在结构二层的外荷载的灵敏度最大,对结构X向位移影响最大,弹性模量的灵敏度小于零表明它对结构X向位移起到负作用。在ANSYS的后处理模块中可以对已定的输入变量进行灵敏度分析,然后判断哪些参数可以实现结构的优化,以达到结构优化的目的[20]。该炼化平台钢框架结构的可靠度是可以接受的,可以对结构非敏感性因子进行优化,即对截面1-8进行优化设计,在保证结构安全可靠的情况下,适当的减少构件的截面面积[21]。以此来达到提高炼化平台钢框架结构设计经济性的目的。
3结论
本文利用有限元软件对炼化平台钢框架结构进行建模,对地震荷载作用下结构的位移进行可靠度分析。炼化平台钢框架结构在地震荷载的作用下,水平最大位移为5.9 mm,远小于规范设计值30 mm,可以看出该框架结构的设计比较保守,钢材比较浪费。由灵敏度图可知,需要将该炼化平台钢框架结构的各梁柱敏感性因子低的截面尺寸进行优化再设计。该炼化平台钢框结构可为以后寻求结构可靠性与经济性的设计方法提供借鉴。
由于本文对于钢框架结构体系并没有进行优化再设计分析,因此,需要对截面优化再设计后的钢框结构做进一步的可靠度分析和研究。
【参考文献】
[1]高剑,王忠凯,潘毅,等.罕遇地震下石化钢结构减震的关键影响因素[J].土木建筑与环境工程,2016,38(1):93-94.
[2]蔡雁蕊.基于灵敏度分析的钢框架支撑结构体系抗侧性能研究[D].广州:广东工业大学,2016.
[3]戚毅婷.基于随机有限元的框架结构可靠性分析[D].昆明:昆明理工大学,2012.
[4]Baalousha H M.Approximation of the exponential integral(well function)using sampling methods[J].Journal of Hydrology,2015,523:278-280.
[5]Olsson A,Sandberg G,Dahlblom O.On Latin hypercube sampling for structural reliability analysis[J].Structural Safety,2003,25(1):47-68.
[6]Olsson A,Sandberg G E.Latin hypercube sampling for stochastic finite element analysis[J].Journal of Engineering Mechanics,2002:128(1):121-125.
[7]中國石化工程建设公司.化工、石化建(构)筑物荷载设计规范:HG/T20674-200[S].北京:化工出版社,2005.
[8]中华人民共和国和城乡建设部.建筑抗震设计规范:GB50011-2010[S].北京:中国建筑工业出版社,2010.
[9]张仙平,胡仁喜,康士廷,等.ANSYS16.0土木工程有限元分析从入门到精通[M].北京:机械工业出版社,2016.
[10]徐鹤山.ANSYS建筑钢结构工程实例分析[M].北京:机械工业出版社,2007.
[11]博弈创作室.ANSYS9.0经典产品基础教程与实例详解[M].北京:中国水利水电出版社,2006.
[12]中国石化工程建设有限公司.石油化工钢结构冷换框架设计规范:SH/T 3077—2012[S].北京:中国石化出版社,2013.
[13]Keshtegar B,Kisi O.M5 model tree and Monte Carlo simulation for efficient structural reliability analysis[J].Applied Mathematical Modelling,2017,48:899-901.
[14]Zhang H,Shayan S,Rasmussen K J R,et al.Systembased design of planar steel frames,I:Reliability framework[J].Journal of Constructional Steel Research,2016,123:135-143.
[15]张伟.结构可靠性理论与应用[M].北京:科学出版社,2008.
[16]赵国藩,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,2000.
[17]王湛,何嘉年.基于蒙特卡罗法的钢框架结构可靠度计算方法的研究[C]//全国钢结构学术年会论文集.中国钢结构协会,2008,10:55-59.
[18]李远瑛,张德生.基于ANSYS的平面框架结构位移可靠度分析[J].湘潭大学自然科学学报,2011,33(2):45-49.
[19]Papadrakakis M,Lagaros N D,Plevris V.Design optimization of steel structures considering uncertainties[J].Engineering Structures,2005,27(9):1408-1418.
[20]Ditlevsen O D,Madsen H O.Structural reliability methods[M].Chichester:John Wiley & Sons,Inc.,1996.
[21]谢镭,于英霞,张伟.基于强度的钢框架可靠性分析与计算[J].炼油技术与工程,2009,39(7):45-49.

