高速列车万向轴不平衡故障检测的形态滤波方法
李奕璠 刘伟渭 林建辉

摘要:结构元素是数学形态学滤波器的重要组成部分,直接影响滤波的精度。针对目前广泛使用的直线和三角结构元素的缺陷,提出一种基于汉明窗的结构元素,对形态滤波方法进行提升,用于高速列车万向轴不平衡故障检测。首先从结构元素的基本构成形式以及频率响应的角度,在理论上对直线和三角结构元素存在的不足进行了分析。再通过对多种常用的窗函数进行比较,论证汉明窗的优势所在,据此构建汉明结构元素,并将其应用于形态滤波中。在万向轴不平衡试验台进行了试验,结果表明:基于汉明结构元素的形态滤波方法能有效地识别出万向轴不平衡引起的基频和倍频故障特征,与传统的三角结构元素相比,此方法更能彰显故障特征。
关键词:故障诊断;高速列车;万向轴;形态滤波;结构元素
中图分类号:TH165+.3;U463.216 文献标志码:A 文章编号:1004-4523(2018)01-0176-07
DOI:10.16385/j.cnki.issn.1004-4523.2018.01.021
引言
万向轴是CRH5型列车传动系统的重要组成部件,其两端通过十字万向节分别与牵引电机和齿轮箱相连。由于万向轴为细长杆状结构,其弯曲和扭转刚度都较小。而传动时,万向轴既要传递牵引力矩,又要适应各种运动关系,在此过程中引起的附加力矩容易导致扭转振动。此外,列车长期运行也会使得万向节轴的磨损间隙增大,导致万向轴偏心。上述因素均可能使万向轴产生不平衡,从而加剧传动系统的振动,加速传动系统万向节和轴承的破坏,危及行车安全。因此,对万向轴工作状态进行监测与诊断很有必要。
目前,诊对万向轴故障诊断的研究不多。文使用第二代小波变化结合奇异值分解的方法对此间题进行了研究,但二代小波存在频率重叠现象,可能无法有效反映故障特征。文使用经验模态分解,根据特征模态分量的能量大小,识别是否存在万向轴不平衡;文同样使用经验模态分解,依据固有模态函数的平均瞬时频率和频谱最大值为特征,判别万向轴故障。然而,文的研究均未考虑经验模态分解中固有的模态混叠问题,而该问题对万向轴故障的判别具有不可忽略的影响。本文使用基于数学形态学滤波的方法對万向轴不平衡问题进行研究。
形态滤波是基于数学形态学变换的非线性滤波方法,它依据待处理信号的局部形态特征,通过一系列形态学变换,将信号与噪声分离。其基本思想是使用一个结构元素,并通过它的连续移动,对原始信号进行处理,以达到提取信号特征、抑制噪声的目的。由此可见,结构元素对分析结果有较大影响。在现有的结构元素中,直线结构元素的构成最为简单且计算量最小,因此,得到了最为广泛的应用。而三角结构元素的形貌与机械振动信号的波形更为相近,其分析精度相对于直线结构元素更高,同样得到了一定的使用。
形态滤波中结构元素的作用类似于传统滤波器的滤波窗,直线结构元素的本质是矩形窗,三角结构元素的本质为三角窗。Mcfadden指出这两种窗函数均具有较大的旁瓣,可能会引起较大的分析误差。因此,有必要构建一种新的结构元素,以提高形态滤波方法的分析精度。为此,本文提出基于汉明结构元素的形态滤波方法,以期实现万向轴故障的有效诊断。
1已有的结构元素及其不足
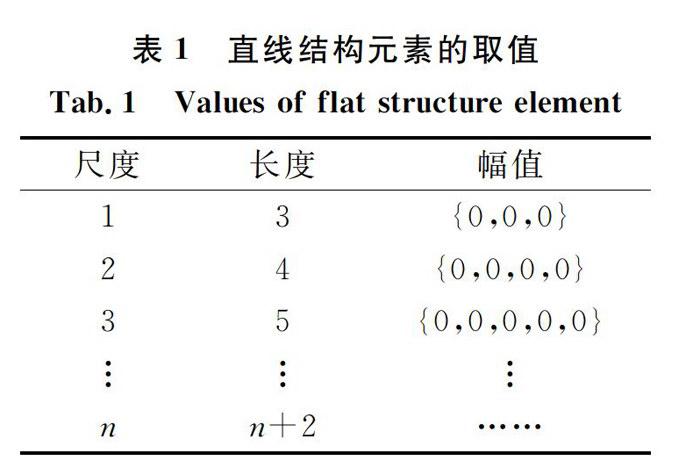
结构元素两大要素分别为长度和幅值。对于直线结构元素,其幅值始终为零,仅存在长度方向上的变化。最简单的直线结构元素可表示为{0,0,0}。直线结构元素的长度和幅度值的相互关系列于表1。由表1可知,直线结构元素在长度上的增量是连续的。
三角结构元素长度和幅值如表2所示。与直线结构元素不同的是,三角结构元素的长度和幅值都会随着尺度的变化而改变。最简单的三角结构元素可表示为{0,1,0)。这里的0和1均表示结构元素的幅值。但是,在实际的使用中,三角结构元素的幅值会依据待分析信号的波形进行调整,表2中的参数ai(i=1,2,…,n)的作用即在于此,ai的具体确定方法可参见文。
文的研究表明三角窗的频域响应函数优于矩形窗。Zhang等在对滚动轴承进行故障诊断中也发现使用三角结构元素的分析效果相比于使用直线结构元素更好。因此,在本文的后续研究中,不再关注直线结构元素。
但是,三角结构元素依然存在明显的问题。从表2可以看到,三角结构元素的长度值始终为一个奇数,这意味着该结构元素在长度方向上的变化不连续,这会导致三角结构元素无法精确地对原始信号进行匹配。借助图1的信号,对此问题进行具体说明。
图1中,信号的采样频率为1000Hz。振动信号的第二个冲击,从0.039到0.049s,总共包含了11个采样点。因此,根据表2,可以使用尺度为5的三角结构元素对其进行处理。然而,对于第一个冲击,从0到0.039s,包含40个采样点,对于这个冲击,究竟应该选择尺度为19的三角结构元素还是选择尺度为20的三角结构元素对其进行处理呢?无论选择哪一个,都无法精确匹配原信号。因为尺度19对应的长度为39个采样点,而尺度20对应的长度为41个采样点。
所以往往自然的就会想到,能否构造偶数个点的三角元素?构造偶数个点的三角结构元素在Matlab里是很容易实现的,但是偶数个点的三角结构元素会使得结构元素的顶部变成扁平状,如图2所示,同样无法精确匹配机械振动信号的冲击特征。因此,在下一部分,研究一种新的结构元素。
2汉明结构元素
许多窗函数都可以被用来构建结构元素。除了矩形窗和三角窗,常见的窗函数还包括汉宁窗、布莱克曼窗、Tukey窗和汉明窗等。为了从中找出最优的窗,从理论上对它们进行分析比较。图3(a)为这些窗函数的时域波形,信号的采样频率为1000Hz,所有窗函数的宽度为2000个采样点,窗函数的数学模型可参见文。将图3(a)所示的窗函数进行快速傅里叶变换,图3(b)为对应的频谱。
评价一个滤波窗的性能好坏主要有以下两个标准:第一,其主瓣宽度应尽可能窄。主瓣宽度定义为从零到频率响应曲线与频率轴的第一个交点之间的距离。从图3(b)可见,Tukey窗和布莱克曼窗的主瓣宽度较大,因此,Tukey窗和布莱克曼窗被排除。而三角窗、汉宁窗和汉明窗具有相同的主瓣宽度。第二,旁瓣高度应尽可能矮。在剩下的三个窗函数中,汉明窗的旁瓣高度最小。因此,汉明窗具有最好的频率响应特性,本文选用汉明窗。
汉明窗可用下式表示
(1)式中L代表窗的长度。根据式(1)构建汉明结构元素。不同尺度下汉明结构元素的值如表3所示。可见,相较于三角结构元素(表2),汉明结构元素的取值是连续的。表3中,ω1(0)≠ω2(0)≠ω3(0)≠…≠ωn(0),ω1(1)≠ω2(1)≠ω3(1)≠…≠ωn(1),以此类推。这是因为对于不同的尺度,窗的长度L发生了改变。
汉明结构元素中另一个重要的参数就是幅值系数bi(i=1,2,…,n),其具体的确定方法如下:
(1)寻找原始信号中所有的极小值点;
(2)计算任意两个相邻极小值点之间的时间间隔;
(3)分别将原始信号中具有同样时间间隔的冲击提取出来,归为一类,每一类冲击信号具有相同的分析尺度;
(4)对于相同尺度的冲击信号,依据3σ原则计算其幅值的统计特征,其中,σ是同一尺度信号的标准差。汉明结构元素在不同尺度下的幅值bi=3σi(i=1,2,…,n)。因为对于机械振动信号来说,幅值大于3σ的部分可以认为其是噪声。
3基于汉明结构元素的形态滤波方法
汉明结构元素的构建完成后,将其应用于形态学运算之中。膨胀和腐蚀是形态学分析中两种最基本的运算。设原始信号为f(n)(n=1,2,…,N),汉明结构元素为g(m)(m=1,2,…,M),且N≥M。f(n)关于g(m)的膨胀和腐蚀分别定义为:
开运算能抑制信号中的正冲击,保留负冲击。而闭运算能保留正冲击,抑制负冲击。为了同时得到两个方向的冲击特征,通过将开、闭运算进行组合,得到差值(DIF)形态滤波器
式(2)~(6)给出的是单一尺度下形态滤波器的处理过程。事实上,只需要按照第二部分的方法确定不同尺度下的结构元素g(m),就能根据式(2)~(6)得到不同尺度下每一个尺度的滤波结果。而多尺度形态滤波器的最终输出为所有尺度滤波结果的算术平均
(7)式中k为多尺度形态滤波器的分析尺度。
4试验分析
为了验证本文方法的效果,在万向轴不平衡试验台(图4)进行了试验。试验中,万向轴一端与齿轮箱相连,齿轮箱由电机驱动。将万向轴另一端支撑座垫高,确保万向轴在垂向存在倾角,以模拟列车实际运行状态。振动传感器安装在齿轮箱上最靠近万向轴的非旋转部位,采样频率20kHz。选用同一型号的两根万向轴进行试验,一根是新轴,一根是存在轻微不平衡的轴,在此将其称之为故障轴。为了将齿轮箱中齿轮啮合频率去除,对采集到的信号进行了1kHz低通滤波。
使用本文方法对万向轴进行故障检测的步骤如下:
(1)考察万向轴振动信号极值点的分布情况,确定每一个冲击对应的采样点数,假设第一个冲击的长度为6个采样点,第二个冲击的长度为4个采样点,等等。有n个冲击,就得到n个结果;
(2)对(1)得到的n个结果进行归类,即将所有长度为6个采样点的冲击归为一类,将所有长度为4个采样点的冲击归为一类,以此类推,并据此得到m类冲击;
(3)按照第二部分的方法对m类冲击分别构建汉明结构元素;
(4)按式(6),使用构建的汉明结构元素,对振动信号进行多尺度形态滤波,得到m个滤波结果;
(5)对m个滤波结果进行算术平均(式(7)),得到多尺度形态滤波器的输出。
(6)对(5)的时域波形进行频谱分析。
4.1正常軸的分析结果
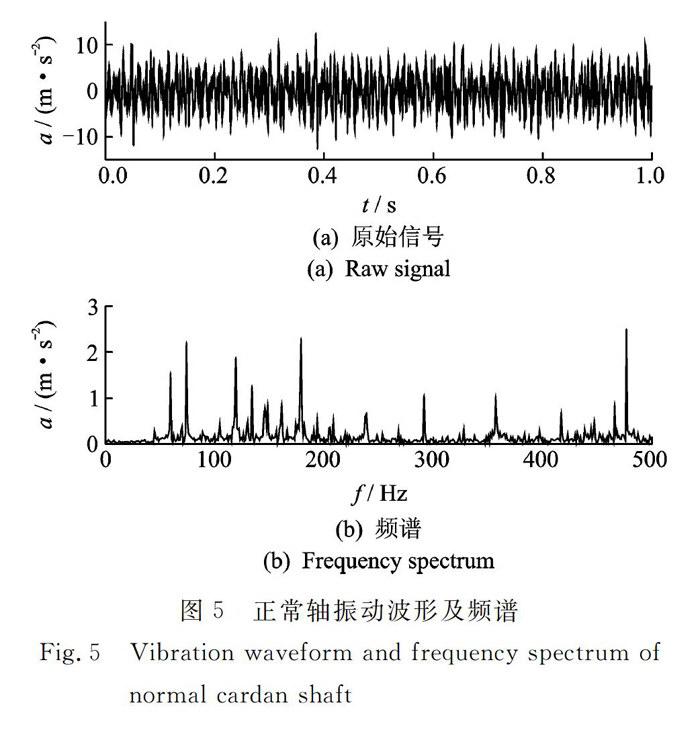
万向轴的转速为880r/min,对应的转频约为15Hz。图5为正常万向轴振动的时间历程曲线和频谱。从图5(b)的频谱中,无法找到万向轴转频。
使用本文方法对正常轴振动信号进行处理。通过计算图5(a)信号极值点的分布发现,原始信号相邻极小值间隔分布在2个采样点到8个采样点之间。2个采样点的时间间隔意味着该冲击共包含3个采样点(根据表3,使用尺度为1的汉明结构元素进行分析),3个采样点的时间间隔意味着此冲击共包含4个采样点(根据表3,使用尺度为2的汉明结构元素进行分析),以此类推。因此,多尺度形态滤波器的最终滤波输出是由尺度为1-7的7个滤波器的滤波结果取平均得到,如图6(a)所示,图6(b)是图6(a)信号的频谱。从图6(b)中可以清楚地识别万向轴转频及其二倍频、四倍频、五倍频和七倍频。
使用基于三角结构元素的多尺度滤波方法对图5(a)所示的信号进行分析。为了进行公平的比较,与图6的分析使用同样的形态学运算。由于原始信号相邻极小值间隔分布在2至8个采样点之间,根据表2,使用尺度1-4的多尺度滤波器进行处理,相应的滤波结果及频谱如图7所示。从图7(b)中可以勉强识别出万向轴的转频及二倍频和四倍频,但频谱中最为突出的频率成分与转频及其倍频毫无关系。对比图6(b)与图7(b)可以看到汉明结构元素在抑制噪声、提取信号特征方面的优势。由于多尺度形态滤波器中,较小的尺度主要用于提取冲击特征,较大的尺度主要用于抑制噪声。对于一个振动信号来说,其极小值点是固定的,而滤波器的尺度的确定完全取决于信号极小值点的分步。三角结构元素的构成(表2)决定了其分析尺度少于汉明结构元素(表3),使得抑制噪声的能力受到了一定程度的消弱,这是其分析效果不如汉明结构元素的重要原因。
4.2故障轴的分析结果
在同样的试验条件下,对存在轻微不平衡故障的万向轴进行了测试,得到的时域波形及频谱如图8所示。从图8(b)的频谱中很难识别出万向轴的转频和倍频。对比图8与5,无论在时域还是频域,正常轴与故障轴的差异均不显著。
使用基于汉明结构元素的多尺度形态滤波方法,对图8(a)的信号进行分析。计算图8(a)信号极值点的分布发现,原始信号相邻极小值间隔分布在2个采样点到9个采样点之间。使用基于汉明结构元素的尺度为1-8的多尺度形态滤波器对此信号进行处理,结果如图9所示。从图9(b)中可以清晰地看到万向轴的转频15Hz和二倍频30Hz、三倍频45Hz、四倍频60Hz和五倍频75Hz。同时,在转频以及二倍频和三倍频处的幅值分别为正常万向轴同一位置(图6(b))幅值的1.15,2.0和2.39倍,而这正是典型的转子不平衡故障特征。
图10为使用三角结构元素对故障轴振动信号进行多尺度形态滤波得到的时域波形和频谱。从图10(b)中可以检测到万向轴转频的二倍频成分,但此频率被噪声污染,与图9(b)相比,故障特征并不突出,这再次说明了汉明结构元素在故障特征提取方面更为有效。
5结论
结构元素直接影响形态滤波的结果,现有的研究一般选用直线或三角结构元素,但它们存在长度变化不连续、频率响应函数欠佳等缺陷。为此,本文提出一种汉明结构元素,并将其应用于多尺度形态滤波器中。利用万向轴台架试验的测试数据对提出的方法进行了验证,结果表明,本文方法能够从齿轮箱测点的振动信号中有效地提取出万向轴振动的特征,识别正常万向轴与存在不平衡的万向轴。相对于基于三角结构元素的多尺度形态滤波器的分析结果,无论是在频谱的识别度,还是特征频率的振动能量都得到了显著增强。



摘要:结构元素是数学形态学滤波器的重要组成部分,直接影响滤波的精度。针对目前广泛使用的直线和三角结构元素的缺陷,提出一种基于汉明窗的结构元素,对形态滤波方法进行提升,用于高速列车万向轴不平衡故障检测。首先从结构元素的基本构成形式以及频率响应的角度,在理论上对直线和三角结构元素存在的不足进行了分析。再通过对多种常用的窗函数进行比较,论证汉明窗的优势所在,据此构建汉明结构元素,并将其应用于形态滤波中。在万向轴不平衡试验台进行了试验,结果表明:基于汉明结构元素的形态滤波方法能有效地识别出万向轴不平衡引起的基频和倍频故障特征,与传统的三角结构元素相比,此方法更能彰显故障特征。
关键词:故障诊断;高速列车;万向轴;形态滤波;结构元素
中图分类号:TH165+.3;U463.216 文献标志码:A 文章编号:1004-4523(2018)01-0176-07
DOI:10.16385/j.cnki.issn.1004-4523.2018.01.021
引言
万向轴是CRH5型列车传动系统的重要组成部件,其两端通过十字万向节分别与牵引电机和齿轮箱相连。由于万向轴为细长杆状结构,其弯曲和扭转刚度都较小。而传动时,万向轴既要传递牵引力矩,又要适应各种运动关系,在此过程中引起的附加力矩容易导致扭转振动。此外,列车长期运行也会使得万向节轴的磨损间隙增大,导致万向轴偏心。上述因素均可能使万向轴产生不平衡,从而加剧传动系统的振动,加速传动系统万向节和轴承的破坏,危及行车安全。因此,对万向轴工作状态进行监测与诊断很有必要。
目前,诊对万向轴故障诊断的研究不多。文使用第二代小波变化结合奇异值分解的方法对此间题进行了研究,但二代小波存在频率重叠现象,可能无法有效反映故障特征。文使用经验模态分解,根据特征模态分量的能量大小,识别是否存在万向轴不平衡;文同样使用经验模态分解,依据固有模态函数的平均瞬时频率和频谱最大值为特征,判别万向轴故障。然而,文的研究均未考虑经验模态分解中固有的模态混叠问题,而该问题对万向轴故障的判别具有不可忽略的影响。本文使用基于数学形态学滤波的方法對万向轴不平衡问题进行研究。
形态滤波是基于数学形态学变换的非线性滤波方法,它依据待处理信号的局部形态特征,通过一系列形态学变换,将信号与噪声分离。其基本思想是使用一个结构元素,并通过它的连续移动,对原始信号进行处理,以达到提取信号特征、抑制噪声的目的。由此可见,结构元素对分析结果有较大影响。在现有的结构元素中,直线结构元素的构成最为简单且计算量最小,因此,得到了最为广泛的应用。而三角结构元素的形貌与机械振动信号的波形更为相近,其分析精度相对于直线结构元素更高,同样得到了一定的使用。
形态滤波中结构元素的作用类似于传统滤波器的滤波窗,直线结构元素的本质是矩形窗,三角结构元素的本质为三角窗。Mcfadden指出这两种窗函数均具有较大的旁瓣,可能会引起较大的分析误差。因此,有必要构建一种新的结构元素,以提高形态滤波方法的分析精度。为此,本文提出基于汉明结构元素的形态滤波方法,以期实现万向轴故障的有效诊断。
1已有的结构元素及其不足
结构元素两大要素分别为长度和幅值。对于直线结构元素,其幅值始终为零,仅存在长度方向上的变化。最简单的直线结构元素可表示为{0,0,0}。直线结构元素的长度和幅度值的相互关系列于表1。由表1可知,直线结构元素在长度上的增量是连续的。
三角结构元素长度和幅值如表2所示。与直线结构元素不同的是,三角结构元素的长度和幅值都会随着尺度的变化而改变。最简单的三角结构元素可表示为{0,1,0)。这里的0和1均表示结构元素的幅值。但是,在实际的使用中,三角结构元素的幅值会依据待分析信号的波形进行调整,表2中的参数ai(i=1,2,…,n)的作用即在于此,ai的具体确定方法可参见文。
文的研究表明三角窗的频域响应函数优于矩形窗。Zhang等在对滚动轴承进行故障诊断中也发现使用三角结构元素的分析效果相比于使用直线结构元素更好。因此,在本文的后续研究中,不再关注直线结构元素。
但是,三角结构元素依然存在明显的问题。从表2可以看到,三角结构元素的长度值始终为一个奇数,这意味着该结构元素在长度方向上的变化不连续,这会导致三角结构元素无法精确地对原始信号进行匹配。借助图1的信号,对此问题进行具体说明。
图1中,信号的采样频率为1000Hz。振动信号的第二个冲击,从0.039到0.049s,总共包含了11个采样点。因此,根据表2,可以使用尺度为5的三角结构元素对其进行处理。然而,对于第一个冲击,从0到0.039s,包含40个采样点,对于这个冲击,究竟应该选择尺度为19的三角结构元素还是选择尺度为20的三角结构元素对其进行处理呢?无论选择哪一个,都无法精确匹配原信号。因为尺度19对应的长度为39个采样点,而尺度20对应的长度为41个采样点。
所以往往自然的就会想到,能否构造偶数个点的三角元素?构造偶数个点的三角结构元素在Matlab里是很容易实现的,但是偶数个点的三角结构元素会使得结构元素的顶部变成扁平状,如图2所示,同样无法精确匹配机械振动信号的冲击特征。因此,在下一部分,研究一种新的结构元素。
2汉明结构元素
许多窗函数都可以被用来构建结构元素。除了矩形窗和三角窗,常见的窗函数还包括汉宁窗、布莱克曼窗、Tukey窗和汉明窗等。为了从中找出最优的窗,从理论上对它们进行分析比较。图3(a)为这些窗函数的时域波形,信号的采样频率为1000Hz,所有窗函数的宽度为2000个采样点,窗函数的数学模型可参见文。将图3(a)所示的窗函数进行快速傅里叶变换,图3(b)为对应的频谱。
评价一个滤波窗的性能好坏主要有以下两个标准:第一,其主瓣宽度应尽可能窄。主瓣宽度定义为从零到频率响应曲线与频率轴的第一个交点之间的距离。从图3(b)可见,Tukey窗和布莱克曼窗的主瓣宽度较大,因此,Tukey窗和布莱克曼窗被排除。而三角窗、汉宁窗和汉明窗具有相同的主瓣宽度。第二,旁瓣高度应尽可能矮。在剩下的三个窗函数中,汉明窗的旁瓣高度最小。因此,汉明窗具有最好的频率响应特性,本文选用汉明窗。
汉明窗可用下式表示
(1)式中L代表窗的长度。根据式(1)构建汉明结构元素。不同尺度下汉明结构元素的值如表3所示。可见,相较于三角结构元素(表2),汉明结构元素的取值是连续的。表3中,ω1(0)≠ω2(0)≠ω3(0)≠…≠ωn(0),ω1(1)≠ω2(1)≠ω3(1)≠…≠ωn(1),以此类推。这是因为对于不同的尺度,窗的长度L发生了改变。
汉明结构元素中另一个重要的参数就是幅值系数bi(i=1,2,…,n),其具体的确定方法如下:
(1)寻找原始信号中所有的极小值点;
(2)计算任意两个相邻极小值点之间的时间间隔;
(3)分别将原始信号中具有同样时间间隔的冲击提取出来,归为一类,每一类冲击信号具有相同的分析尺度;
(4)对于相同尺度的冲击信号,依据3σ原则计算其幅值的统计特征,其中,σ是同一尺度信号的标准差。汉明结构元素在不同尺度下的幅值bi=3σi(i=1,2,…,n)。因为对于机械振动信号来说,幅值大于3σ的部分可以认为其是噪声。
3基于汉明结构元素的形态滤波方法
汉明结构元素的构建完成后,将其应用于形态学运算之中。膨胀和腐蚀是形态学分析中两种最基本的运算。设原始信号为f(n)(n=1,2,…,N),汉明结构元素为g(m)(m=1,2,…,M),且N≥M。f(n)关于g(m)的膨胀和腐蚀分别定义为:
开运算能抑制信号中的正冲击,保留负冲击。而闭运算能保留正冲击,抑制负冲击。为了同时得到两个方向的冲击特征,通过将开、闭运算进行组合,得到差值(DIF)形态滤波器
式(2)~(6)给出的是单一尺度下形态滤波器的处理过程。事实上,只需要按照第二部分的方法确定不同尺度下的结构元素g(m),就能根据式(2)~(6)得到不同尺度下每一个尺度的滤波结果。而多尺度形态滤波器的最终输出为所有尺度滤波结果的算术平均
(7)式中k为多尺度形态滤波器的分析尺度。
4试验分析
为了验证本文方法的效果,在万向轴不平衡试验台(图4)进行了试验。试验中,万向轴一端与齿轮箱相连,齿轮箱由电机驱动。将万向轴另一端支撑座垫高,确保万向轴在垂向存在倾角,以模拟列车实际运行状态。振动传感器安装在齿轮箱上最靠近万向轴的非旋转部位,采样频率20kHz。选用同一型号的两根万向轴进行试验,一根是新轴,一根是存在轻微不平衡的轴,在此将其称之为故障轴。为了将齿轮箱中齿轮啮合频率去除,对采集到的信号进行了1kHz低通滤波。
使用本文方法对万向轴进行故障检测的步骤如下:
(1)考察万向轴振动信号极值点的分布情况,确定每一个冲击对应的采样点数,假设第一个冲击的长度为6个采样点,第二个冲击的长度为4个采样点,等等。有n个冲击,就得到n个结果;
(2)对(1)得到的n个结果进行归类,即将所有长度为6个采样点的冲击归为一类,将所有长度为4个采样点的冲击归为一类,以此类推,并据此得到m类冲击;
(3)按照第二部分的方法对m类冲击分别构建汉明结构元素;
(4)按式(6),使用构建的汉明结构元素,对振动信号进行多尺度形态滤波,得到m个滤波结果;
(5)对m个滤波结果进行算术平均(式(7)),得到多尺度形态滤波器的输出。
(6)对(5)的时域波形进行频谱分析。
4.1正常軸的分析结果
万向轴的转速为880r/min,对应的转频约为15Hz。图5为正常万向轴振动的时间历程曲线和频谱。从图5(b)的频谱中,无法找到万向轴转频。
使用本文方法对正常轴振动信号进行处理。通过计算图5(a)信号极值点的分布发现,原始信号相邻极小值间隔分布在2个采样点到8个采样点之间。2个采样点的时间间隔意味着该冲击共包含3个采样点(根据表3,使用尺度为1的汉明结构元素进行分析),3个采样点的时间间隔意味着此冲击共包含4个采样点(根据表3,使用尺度为2的汉明结构元素进行分析),以此类推。因此,多尺度形态滤波器的最终滤波输出是由尺度为1-7的7个滤波器的滤波结果取平均得到,如图6(a)所示,图6(b)是图6(a)信号的频谱。从图6(b)中可以清楚地识别万向轴转频及其二倍频、四倍频、五倍频和七倍频。
使用基于三角结构元素的多尺度滤波方法对图5(a)所示的信号进行分析。为了进行公平的比较,与图6的分析使用同样的形态学运算。由于原始信号相邻极小值间隔分布在2至8个采样点之间,根据表2,使用尺度1-4的多尺度滤波器进行处理,相应的滤波结果及频谱如图7所示。从图7(b)中可以勉强识别出万向轴的转频及二倍频和四倍频,但频谱中最为突出的频率成分与转频及其倍频毫无关系。对比图6(b)与图7(b)可以看到汉明结构元素在抑制噪声、提取信号特征方面的优势。由于多尺度形态滤波器中,较小的尺度主要用于提取冲击特征,较大的尺度主要用于抑制噪声。对于一个振动信号来说,其极小值点是固定的,而滤波器的尺度的确定完全取决于信号极小值点的分步。三角结构元素的构成(表2)决定了其分析尺度少于汉明结构元素(表3),使得抑制噪声的能力受到了一定程度的消弱,这是其分析效果不如汉明结构元素的重要原因。
4.2故障轴的分析结果
在同样的试验条件下,对存在轻微不平衡故障的万向轴进行了测试,得到的时域波形及频谱如图8所示。从图8(b)的频谱中很难识别出万向轴的转频和倍频。对比图8与5,无论在时域还是频域,正常轴与故障轴的差异均不显著。
使用基于汉明结构元素的多尺度形态滤波方法,对图8(a)的信号进行分析。计算图8(a)信号极值点的分布发现,原始信号相邻极小值间隔分布在2个采样点到9个采样点之间。使用基于汉明结构元素的尺度为1-8的多尺度形态滤波器对此信号进行处理,结果如图9所示。从图9(b)中可以清晰地看到万向轴的转频15Hz和二倍频30Hz、三倍频45Hz、四倍频60Hz和五倍频75Hz。同时,在转频以及二倍频和三倍频处的幅值分别为正常万向轴同一位置(图6(b))幅值的1.15,2.0和2.39倍,而这正是典型的转子不平衡故障特征。
图10为使用三角结构元素对故障轴振动信号进行多尺度形态滤波得到的时域波形和频谱。从图10(b)中可以检测到万向轴转频的二倍频成分,但此频率被噪声污染,与图9(b)相比,故障特征并不突出,这再次说明了汉明结构元素在故障特征提取方面更为有效。
5结论
结构元素直接影响形态滤波的结果,现有的研究一般选用直线或三角结构元素,但它们存在长度变化不连续、频率响应函数欠佳等缺陷。为此,本文提出一种汉明结构元素,并将其应用于多尺度形态滤波器中。利用万向轴台架试验的测试数据对提出的方法进行了验证,结果表明,本文方法能够从齿轮箱测点的振动信号中有效地提取出万向轴振动的特征,识别正常万向轴与存在不平衡的万向轴。相对于基于三角结构元素的多尺度形态滤波器的分析结果,无论是在频谱的识别度,还是特征频率的振动能量都得到了显著增强。

