有限长周期支撑结构贝叶斯概率损伤识别研究
尹涛 尹孟林 贾晓健

摘要:提出了一种有限长周期支撑结构损伤概率识别方法。基于特征波导纳原理,分析谐调与存在单一扰乱周期支撑结构的自由波传播规律,建立含单扰乱周期支撑结构的频率特征方程。提出一种无量纲自振频率概念,并运用敏感性分析方法,建立有限长周期支撑结构无量纲自振频率相对于基本周期单元刚度变化敏感性矩阵的一般形式,分析表明所提出无量纲自振频率及其敏感性矩阵与周期支撑结构具体几何材料参数无关,避免敏感性分析对于精确有限元模型的依赖。结合贝叶斯理论与马尔科夫链蒙特卡洛(MCMC)模拟算法,实现基于测量自振频率变化的有限长周期支撑结构单元损伤的概率识别。通过对一含螺栓接头的周期支撑梁实验室模型开展研究,对提出方法的正确性与有效性进行验证。
关键词:周期支撑结构;概率损伤识别;敏感性分析;特征波导纳;贝叶斯理论
中图分类号:TB123;0346.5 文献标志码:A 文章编号:1004-4523(2018)01-0091-11
DOI:10.16385/j.cnki.issn.1004-4523.2018.01.011
引言
近些年来,周期结构在工程领域中获得了广泛的应用,如复合材料层合结构、航天器太阳能电池帆板、超高层建筑、多跨连续桥梁、铁路轨道系统、高速铁路弓网系统以及长输油气管线等都可视作由相同子结构首尾串联而成的链状周期结构系统。周期结构具有独特的带隙(即频率通带和阻带)现象,其表现在当振动波处在结构的频率通带范围内时,波能传遍整个结构而不发生能量和振幅的衰减,而当波处在结构的频率阻带范围时,波将发生能量与振幅衰减,而不能传遍整个结构。此外,结构的周期特性使得对其动力学分析具有显著优势,即对其自由振动进行精确的波动分析不要求对结构进行完全的模拟,利用周期结构这一特性,可以简化分析过程,提高计算效率。目前国内外对周期结构的研究工作大都集中于其带隙特性以及波动局部化等特殊力学特性上,主要利用这一特殊性质指导周期结构的振动控制及优化设计等研究,而对于周期结构损伤检测的研究工作尚鲜见报道。
结构发生损伤时通常会导致其局部刚度降低,进而影响其动力特征参数,结构损伤识别的动力法正是利用测量动力特征参数变化来反演结构刚度降低发生的部位及其程度。其中,敏感性分析方法基于动力特征参数对结构模型参数变化的敏感性分析以实现结构损伤动力识别,该类方法概念明确且易于实施,因而基于实测动力特征参数变化敏感性分析的结构损伤检测一直受到关注。该类方法实施的关键在于选取可测且对结构损伤敏感的动力特征参数,而结构模态参数在实际工程中相对容易测量且对结构整体刚度改变较为敏感,因而应用较广泛,报道较多的损伤检测模态参数有结构的固有频率、模态振型及模态振型曲率等。例如,cawley和Adares最早将固有频率敏感性分析运用于结构损伤识别研究,通过固有频率敏感性分析对简单结构的损伤位置和损伤程度进行了识别;wahab和Ro-eck提出了基于振型曲率敏感性分析的损伤识别方法,并将其应用于实际桥梁结构;chang和Kim针对某实际桁架桥结构,研究比较了固有频率、模态振型、模态置信准则(MAC)及坐标模态置信準则(COMAC)等对于桁架桥竖向撑杆损伤的敏感性。孙国等提出基于模态误差函数灵敏度分析的损伤识别方法,通过将少数优势单元参数的提取,实现逐次扩增的参数更新策略;尹涛等结合自振频率、模态振型及模态应变能的敏感性分析方法与摄动法开展了框架结构的概率损伤识别研究。
应指出,由于未考虑周期结构特性,将以上敏感性分析方法直接应用于大型周期结构将存在计算量大、识别效率低等问题。此外,目前敏感性方法通常依赖于较准确的结构参数化模型,即需要通过健康结构建模获得结构模态参数对损伤参数的敏感性系数,而对于无法准确获知结构健康状态下几何物理参数的情况,以上方法的应用就存在明显局限性。Zhu和Wu运用波传播理论获得了周期弹簧-质量系统的频率特征方程,并基于固有频率敏感性分析对多高层建筑模型进行了损伤识别,但该方法应用范围仅限于能简化为弹簧-质量系统的结构,实际适用范围受到较大限制,且该方法为确定性方法,未考虑测量噪声等不确定性因素对识别损伤结果的影响。
本文在文献基础上,运用波传播方法分析了具有N个单元的周期支撑结构的自由振动特性,提出一种无量纲自振频率概念,并得到无量纲自振频率与基本周期单元整体刚度变化率之间的关系。建立无量纲自振频率变化率对单元损伤的敏感性识别方程组,并采用贝叶斯理论进行分析求解,得出损伤参数的最大可能值,同时显式评估各周期单元损伤程度的不确定性,进而定量判别各周期单元的损伤概率,实现周期支撑结构的概率损伤识别。此外,本文周期支撑结构无量纲自振频率的敏感性不依赖于结构的具体几何材料参数(如质量密度、弹性模量、单元长度及横截面形状尺寸等),具有显著的优越性和实用性。通过对一含螺栓接头的周期支撑梁实验模型开展损伤识别研究,对本文方法的正确性进行验证。
1理论背景
1.1无限长谐调单耦合周期系统波传播
各基本周期单元左右两侧耦合坐标点处位移和力的相互关系可以表示为
联立公式(1)和(2)可得
由式(3)可得到导纳与波传播常数之间的关系
进一步可得到传递波和反射波对应的特征波导纳分别为
1.2含单扰乱的单耦合周期支撑结构频率特征方程
图2表示具有N个质点的单耦合有限周期结构,C和D为任意边界,j单元出现扰乱(或损伤),假设在左边界C施加激励力,入射波将向扰乱单元j传播并对其产生影响。当传播到扰乱单元后,一部分被反射回振源,另一部分则穿过扰乱单元继续传播至另一边界D并再次部分反射,因此,波的运动过程可以表示为人射波运动与反射波运动的叠加,在扰乱单元左边界A引起的总位移为
则扰乱单元两端力与位移之间可通过单元导纳进行联系,即
理论上,式(13)中给出的频率特征方程适用于任何存在单扰乱的单耦合周期结构体系,但文献基于该理论提出的损伤识别方法仅适用于简单的弹簧一质量系统,应用范围受到较大限制,本文将该理论推广应用于解决更具一般性的周期支撑结构损伤识别问题。图3表示本文所研究的具有N个基本周期单元的周期支撑结构,其中假定第j单元为损伤单元,损伤程度以单元整体刚度降低来表征。
周期支撑结构中健康周期单元的直接导纳与间接导纳可以分别表示为
通过式(23)描述的频率特征方程能计算得到健康状态下周期支撑结构的各阶无量纲自振频率值。
1.3敏感性识别方程组建立与贝叶斯概率识别
在多单元损伤情况下,任意阶无量纲自振频率变化可近似为单损伤引起无量纲自振频率变化的线性叠加,若忽略高次项,则损伤引起的总变化率为
实际应用中,周期支撑结构损伤前后固有频率测量值不可避免地存在噪声,将导致与实测值对应的无量纲频率变化率与敏感性预测结果产生偏差,即
本文基于贝叶斯理论进行概率损伤识别,给出周期支撑结构各单元损伤参数的最大可能值,同时显式评估各单元损伤程度的不确定性,进而判别各单元损伤概率,所得结果更具合理性。定义数据集D为损伤前后重复测量获得的Ns组无量纲频率相对变化率(通过式(19)计算),依据贝叶斯定理,在给定测量数据集D与周期结构模型CN的条件下,损伤参数△θ的后验概率密度函数可以表示为
将本文贝叶斯概率识别方法主要流程概括如下:
1)假定未知参数先验分布的均值与方差,依式(31)与(32)形成先验分布p(△θ|CN);
2)通过重复模态试验获得周期结构损伤前后的NS组自振频率向量,再依式(19)计算得到相应组数的无量纲频率相对变化率向量;
3)基于步骤2),根据式(26)与(30)形成误差函数J1(△θ;D,CD),再通过式(29)计算似然函数p(D|△θ,CD);
4)结合步骤1)和3),通过式(28)形成未知参数A0的后验概率密度分布函数p(△θ|C,CD);
5)运用MCMC算法在步骤4)所定义的后验分布中对AO进行抽样,获得后验分布在参数空间θ中的样本△θ(i);
7)令损伤阈值d在取值区间[0,1)内以一定步长变化,在各离散阈值点处通过式(37)分别计算获得周期支撑结构第j单元发生损伤的概率。
2模型实验验证
本节通过含螺栓接头的实验室五跨周期支撑梁模型来验证本文提出的方法。如图4(a)所示,该周期梁结构模型由5段均匀铝质扁梁通过跨中螺栓连接而形成,整段梁结构等间距支撑于6个钢质支座上,包含1个固定支座(最左端)与5个支撑支座,每个支座均通过螺栓与槽钢底座连接。其中,固定支座通过上下两根钢条将铝梁最左端钳固以模拟周期梁左端固定边界,而其余各支座则通过钢质转动轴承限制铝梁在支座处的竖向位移来实现一般支撑边界条件,两种形式支座局部构造分别如图4(b)与图4(c)所示。此外,将相邻两支座之间的梁段视为一个基本周期单元(如图4(d)所示),且规定梁最左端固定支撑与其相邻支撑之间梁段为1号周期单元,从左至右依次为2,3,4,5号周期单元。每个基本周期单元跨中均通过上下两块等尺寸铝质夹片与4个螺栓将各相邻梁段连接成整体,如图4(e)所示,全梁共5个螺栓接头。视整段梁所有跨中螺栓全部紧固为健康基准状态,而通过松动某基本周期单元跨中接头螺栓以降低接头刚度,进而模拟该周期单元的损伤状态。该周期铝梁的具体几何与材料参数由表1给出。
本文采用的实验装置系统如图5所示,其主要由实验梁模型、IEPE型加速度计(KT—1000LC)、测试导线、八通道信号采集卡(MPS-140801)、冲击力锤、笔记本电脑以及基于LabVIEw编程的信号采集软件所构成,该软件能实现加速度信号的实时显示、回放以及存储等基本功能。加速度传感器布置在距每跨梁段中部接头6cm处,全梁共布设5个,整体与局部布置方式分别如图5(a)与图5(b)所示。通过冲击力锤对周期梁施加竖向冲击荷载,其作用点距离第一跨右支撑15cm处,如圖5(c)所示。本实验采样频率设为500Hz,以满足采样定理,且每次采样时长约为10s,以包含完整的自由响应信号时间段,实验模态参数识别利用采集的自由响应数据基于自编ERA算法实现。
本次实验共考虑了两种损伤工况,每种工况均有5个待识别损伤参数,即△θ={△θ1,△θ2,…,△θ25}T,分别对应各梁跨的整体刚度降低率。其中,第一种工况仅松动第4号周期梁段跨中铝质夹片的部分螺栓,为单损伤工况;第二种为双损伤工况,其在前一工况基础上进一步松动第5号周期梁段跨中接头的部分螺栓,即此工况下第4,5号周期梁段同时发生损伤。应该指出,本文针对周期支撑梁结构所提出的损伤识别方法其识别对象为各跨梁段的整体刚度降低,因此,本实验通过调整部分周期梁段接头螺栓松紧而造成的梁段跨中局部刚度降低程度,在本文方法框架内将通过其导致的梁段整体刚度降低来反映。
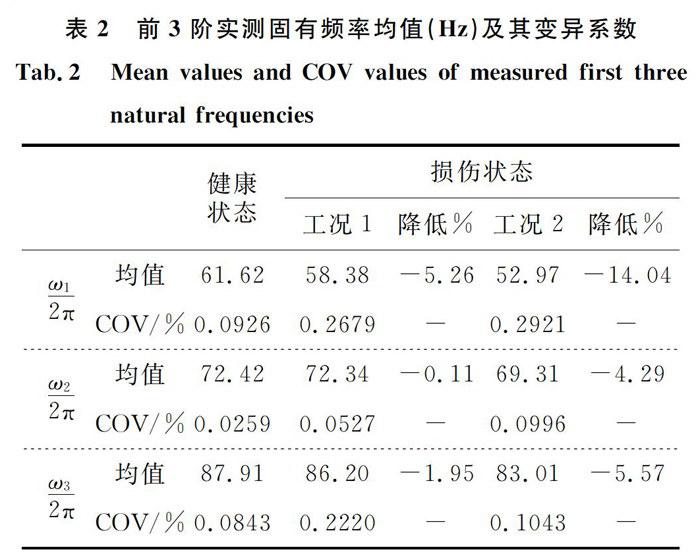
通过重复模态试验,分别获得周期结构健康状态及各损伤工况下的前3阶固有频率各10组,如图6所示,即Nt=3,Ns=10。从图中可以明显看出,频域区间被此3阶模态分成3条明显的条带,各频带内各状态下重复测量所得的模态频率值波动很小,测量结果较稳定。具体地,工况1所设置的损伤对结构第2阶固有频率基本无影响,而对于第3阶模态的影响也较小,相比之下,工况2所对应损伤情况对于后两阶模态频率都有相对明显影响。同时,两种损伤工况对第1阶固有频率影响都较明显,尤其是工况2。此外,为定量反映各损伤情况下模态频率的大小及变化程度,表2给出各工况下重复测量获得的前3阶固有频率均值及变异系数(COV)结果。可以看出,该表给出结果与图6体现的规律相符,同时也反映本次模态试验获得的相关固有频率实测结果的不确定性程度较低。
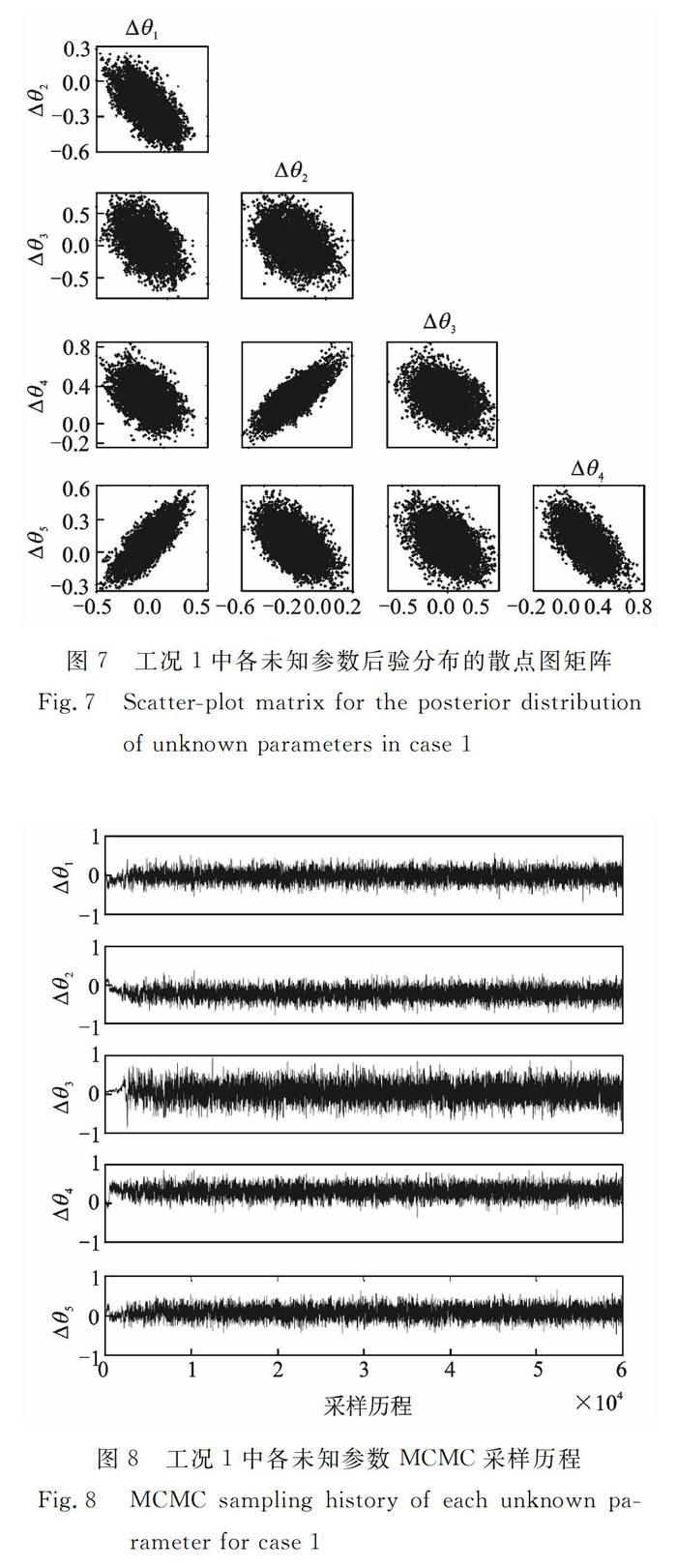
基于获得的模态试验数据,采用MCMC方法进行损伤参数AO的后验分布采样,先验分布取为零均值高斯分布,模拟次数NMC设为6×104,且取后半部分稳定样本进行参数估计。以工况1为例,图7和图8分别表示各未知参数后验分布样本的散点图矩阵与采样历程。其中,图7中给出的散点图矩阵为散点图的高维扩展,一定程度上克服了在平面上展示高维数据的困难,直观反映出各损伤参数之间的相关性,如△θ1与△θ5,以及△θ2与△θ4之间具有较明显的线性正相关性。实事上,固有频率作为结构整体参数,其对结构对称位置的损伤判定存在困难。尽管本文五跨周期支撑梁实验模型左端边界固定,但整体结构仍保留有一定程度的对称性特征,而给△θ1与△θ5(或△θ2与△θ4)的同时识别带来一定困难。此外,从图8可以明显看出,MCMC模拟中各参数收敛情况较好,且处于周期梁结构中间位置的第3跨损伤参数△θ3的样本波动较大,反映其后验估计的不确定性程度较大。
事实上,本文提出的损伤概率判定条件(即式(37))建立在未知损伤参数后验样本近似服从正态分布基础之上,因而图9以工况1为例对MCMC后验样本的正态分布特征进行检验。该图表示通过MCMC方法采样获得的未知参数后验分布样本的正态分布概率校验图,其很明显地反映各参数后验分布稳定样本点绝大部分落在各条斜直线上,表明各未知参数的穩定后验样本服从正态分布。同时,也可以明显看出损伤参数A03样本斜率大于其余参数,表明该参数后验估计的不确定性较其余未知参数大,与图8中的现象吻合,工况2所得规律与工况1类似。
图10表示两工况下通过MCMC方法抽样获得的各损伤参数后验样本的统计直方图与相应正态分布拟合曲线,该图进一步表明损伤参数的稳定后验样本服从正态分布,这与图9给出的概率分布校验结果相符。同时,从图10中也可以看出两种工况下损伤参数A03后验分布的标准差较其他参数大,而其余参数不确定性程度比较接近,这与此前获得结论相一致。此外,依式(19),(24)以及(25)可知,本文各周期梁段损伤参数△θj(j=1,2,…,N,N=5)识别结果大于0即认为该参数对应梁段理论上发生损伤。对于工况1,图10(a)反映出损伤参数△θ4后验样本均值相对于其余参数明显大于0,这表明第4号梁段整体上很可能发生刚度降低。工况2结果类似,图10(b)表明损伤参数△θ4与△θ5所对应梁段发生整体刚度损失的可能性较大。
应该指出,图10给出结果从均值角度反映出各工况下的实际损伤部位与其近似损伤程度,但其判定是以0为基准。从概率论与数理统计理论上看,以0作为损伤与否的判定基准其可靠性值得商榷。针对该问题,本文设置在给定域内变化的损伤程度阈值d,计算损伤参数的最可能识别值超过该阈值的概率,以合理反映不同阈值下的损伤发生概率,其计算结果如图11所示。从该图中可以明显看出,两种工况下对应于不同损伤程度阈值的各损伤参数以损伤出现的概率大小表征,且损伤概率随损伤程度阈值增加而逐渐降低。同时,工况1中实际发生损伤的第4号周期单元(对应损伤参数△θ4)与工况2中实际发生损伤的第4,5号周期单元(对应损伤参数△θ4与△θ5)在不同损伤程度阈值下均被明显揭示,此损伤判别结果更具合理性。
3结论
提出了一种针对大型周期支撑结构的动力损伤识别有效方法。基于特征波导纳原理与敏感性分析方法,建立有限长周期支撑结构无量纲自振频率敏感性矩阵的一般形式,并结合贝叶斯理论与MCMC模拟方法实现概率损伤识别,以周期支撑梁实验室模型试验对本文方法进行验证。研究结果表明,利用周期支撑结构的固有周期特性,提出的无量纲自振频率及推导的相应敏感性矩阵仅与周期单元总数和结构损伤所处单元位置有关,而与周期结构其他几何材料参数无关,极大地简化了复杂周期支撑结构频率敏感性分析过程,同时也避免了实际应用中损伤敏感性分析计算对于结构准确模型参数的依赖,显著提高了本文损伤识别方法的有效性与实用性。通过设置损伤阈值,本文基于贝叶斯理论的识别方法能给出各单元发生损伤的概率,提高了损伤识别结果评估的合理性与可靠性。本文针对周期支撑梁结构提出的损伤识别方法的识别对象为各跨梁段的整体刚度降低,因而,在本文方法框架内,本次实验通过调整周期梁段接头螺栓松紧而造成的梁段跨中局部刚度改变程度,是通过其引起的梁段整体刚度降低程度来反映。



摘要:提出了一种有限长周期支撑结构损伤概率识别方法。基于特征波导纳原理,分析谐调与存在单一扰乱周期支撑结构的自由波传播规律,建立含单扰乱周期支撑结构的频率特征方程。提出一种无量纲自振频率概念,并运用敏感性分析方法,建立有限长周期支撑结构无量纲自振频率相对于基本周期单元刚度变化敏感性矩阵的一般形式,分析表明所提出无量纲自振频率及其敏感性矩阵与周期支撑结构具体几何材料参数无关,避免敏感性分析对于精确有限元模型的依赖。结合贝叶斯理论与马尔科夫链蒙特卡洛(MCMC)模拟算法,实现基于测量自振频率变化的有限长周期支撑结构单元损伤的概率识别。通过对一含螺栓接头的周期支撑梁实验室模型开展研究,对提出方法的正确性与有效性进行验证。
关键词:周期支撑结构;概率损伤识别;敏感性分析;特征波导纳;贝叶斯理论
中图分类号:TB123;0346.5 文献标志码:A 文章编号:1004-4523(2018)01-0091-11
DOI:10.16385/j.cnki.issn.1004-4523.2018.01.011
引言
近些年来,周期结构在工程领域中获得了广泛的应用,如复合材料层合结构、航天器太阳能电池帆板、超高层建筑、多跨连续桥梁、铁路轨道系统、高速铁路弓网系统以及长输油气管线等都可视作由相同子结构首尾串联而成的链状周期结构系统。周期结构具有独特的带隙(即频率通带和阻带)现象,其表现在当振动波处在结构的频率通带范围内时,波能传遍整个结构而不发生能量和振幅的衰减,而当波处在结构的频率阻带范围时,波将发生能量与振幅衰减,而不能传遍整个结构。此外,结构的周期特性使得对其动力学分析具有显著优势,即对其自由振动进行精确的波动分析不要求对结构进行完全的模拟,利用周期结构这一特性,可以简化分析过程,提高计算效率。目前国内外对周期结构的研究工作大都集中于其带隙特性以及波动局部化等特殊力学特性上,主要利用这一特殊性质指导周期结构的振动控制及优化设计等研究,而对于周期结构损伤检测的研究工作尚鲜见报道。
结构发生损伤时通常会导致其局部刚度降低,进而影响其动力特征参数,结构损伤识别的动力法正是利用测量动力特征参数变化来反演结构刚度降低发生的部位及其程度。其中,敏感性分析方法基于动力特征参数对结构模型参数变化的敏感性分析以实现结构损伤动力识别,该类方法概念明确且易于实施,因而基于实测动力特征参数变化敏感性分析的结构损伤检测一直受到关注。该类方法实施的关键在于选取可测且对结构损伤敏感的动力特征参数,而结构模态参数在实际工程中相对容易测量且对结构整体刚度改变较为敏感,因而应用较广泛,报道较多的损伤检测模态参数有结构的固有频率、模态振型及模态振型曲率等。例如,cawley和Adares最早将固有频率敏感性分析运用于结构损伤识别研究,通过固有频率敏感性分析对简单结构的损伤位置和损伤程度进行了识别;wahab和Ro-eck提出了基于振型曲率敏感性分析的损伤识别方法,并将其应用于实际桥梁结构;chang和Kim针对某实际桁架桥结构,研究比较了固有频率、模态振型、模态置信准则(MAC)及坐标模态置信準则(COMAC)等对于桁架桥竖向撑杆损伤的敏感性。孙国等提出基于模态误差函数灵敏度分析的损伤识别方法,通过将少数优势单元参数的提取,实现逐次扩增的参数更新策略;尹涛等结合自振频率、模态振型及模态应变能的敏感性分析方法与摄动法开展了框架结构的概率损伤识别研究。
应指出,由于未考虑周期结构特性,将以上敏感性分析方法直接应用于大型周期结构将存在计算量大、识别效率低等问题。此外,目前敏感性方法通常依赖于较准确的结构参数化模型,即需要通过健康结构建模获得结构模态参数对损伤参数的敏感性系数,而对于无法准确获知结构健康状态下几何物理参数的情况,以上方法的应用就存在明显局限性。Zhu和Wu运用波传播理论获得了周期弹簧-质量系统的频率特征方程,并基于固有频率敏感性分析对多高层建筑模型进行了损伤识别,但该方法应用范围仅限于能简化为弹簧-质量系统的结构,实际适用范围受到较大限制,且该方法为确定性方法,未考虑测量噪声等不确定性因素对识别损伤结果的影响。
本文在文献基础上,运用波传播方法分析了具有N个单元的周期支撑结构的自由振动特性,提出一种无量纲自振频率概念,并得到无量纲自振频率与基本周期单元整体刚度变化率之间的关系。建立无量纲自振频率变化率对单元损伤的敏感性识别方程组,并采用贝叶斯理论进行分析求解,得出损伤参数的最大可能值,同时显式评估各周期单元损伤程度的不确定性,进而定量判别各周期单元的损伤概率,实现周期支撑结构的概率损伤识别。此外,本文周期支撑结构无量纲自振频率的敏感性不依赖于结构的具体几何材料参数(如质量密度、弹性模量、单元长度及横截面形状尺寸等),具有显著的优越性和实用性。通过对一含螺栓接头的周期支撑梁实验模型开展损伤识别研究,对本文方法的正确性进行验证。
1理论背景
1.1无限长谐调单耦合周期系统波传播
各基本周期单元左右两侧耦合坐标点处位移和力的相互关系可以表示为
联立公式(1)和(2)可得
由式(3)可得到导纳与波传播常数之间的关系
进一步可得到传递波和反射波对应的特征波导纳分别为
1.2含单扰乱的单耦合周期支撑结构频率特征方程
图2表示具有N个质点的单耦合有限周期结构,C和D为任意边界,j单元出现扰乱(或损伤),假设在左边界C施加激励力,入射波将向扰乱单元j传播并对其产生影响。当传播到扰乱单元后,一部分被反射回振源,另一部分则穿过扰乱单元继续传播至另一边界D并再次部分反射,因此,波的运动过程可以表示为人射波运动与反射波运动的叠加,在扰乱单元左边界A引起的总位移为
则扰乱单元两端力与位移之间可通过单元导纳进行联系,即
理论上,式(13)中给出的频率特征方程适用于任何存在单扰乱的单耦合周期结构体系,但文献基于该理论提出的损伤识别方法仅适用于简单的弹簧一质量系统,应用范围受到较大限制,本文将该理论推广应用于解决更具一般性的周期支撑结构损伤识别问题。图3表示本文所研究的具有N个基本周期单元的周期支撑结构,其中假定第j单元为损伤单元,损伤程度以单元整体刚度降低来表征。
周期支撑结构中健康周期单元的直接导纳与间接导纳可以分别表示为
通过式(23)描述的频率特征方程能计算得到健康状态下周期支撑结构的各阶无量纲自振频率值。
1.3敏感性识别方程组建立与贝叶斯概率识别
在多单元损伤情况下,任意阶无量纲自振频率变化可近似为单损伤引起无量纲自振频率变化的线性叠加,若忽略高次项,则损伤引起的总变化率为
实际应用中,周期支撑结构损伤前后固有频率测量值不可避免地存在噪声,将导致与实测值对应的无量纲频率变化率与敏感性预测结果产生偏差,即
本文基于贝叶斯理论进行概率损伤识别,给出周期支撑结构各单元损伤参数的最大可能值,同时显式评估各单元损伤程度的不确定性,进而判别各单元损伤概率,所得结果更具合理性。定义数据集D为损伤前后重复测量获得的Ns组无量纲频率相对变化率(通过式(19)计算),依据贝叶斯定理,在给定测量数据集D与周期结构模型CN的条件下,损伤参数△θ的后验概率密度函数可以表示为
将本文贝叶斯概率识别方法主要流程概括如下:
1)假定未知参数先验分布的均值与方差,依式(31)与(32)形成先验分布p(△θ|CN);
2)通过重复模态试验获得周期结构损伤前后的NS组自振频率向量,再依式(19)计算得到相应组数的无量纲频率相对变化率向量;
3)基于步骤2),根据式(26)与(30)形成误差函数J1(△θ;D,CD),再通过式(29)计算似然函数p(D|△θ,CD);
4)结合步骤1)和3),通过式(28)形成未知参数A0的后验概率密度分布函数p(△θ|C,CD);
5)运用MCMC算法在步骤4)所定义的后验分布中对AO进行抽样,获得后验分布在参数空间θ中的样本△θ(i);
7)令损伤阈值d在取值区间[0,1)内以一定步长变化,在各离散阈值点处通过式(37)分别计算获得周期支撑结构第j单元发生损伤的概率。
2模型实验验证
本节通过含螺栓接头的实验室五跨周期支撑梁模型来验证本文提出的方法。如图4(a)所示,该周期梁结构模型由5段均匀铝质扁梁通过跨中螺栓连接而形成,整段梁结构等间距支撑于6个钢质支座上,包含1个固定支座(最左端)与5个支撑支座,每个支座均通过螺栓与槽钢底座连接。其中,固定支座通过上下两根钢条将铝梁最左端钳固以模拟周期梁左端固定边界,而其余各支座则通过钢质转动轴承限制铝梁在支座处的竖向位移来实现一般支撑边界条件,两种形式支座局部构造分别如图4(b)与图4(c)所示。此外,将相邻两支座之间的梁段视为一个基本周期单元(如图4(d)所示),且规定梁最左端固定支撑与其相邻支撑之间梁段为1号周期单元,从左至右依次为2,3,4,5号周期单元。每个基本周期单元跨中均通过上下两块等尺寸铝质夹片与4个螺栓将各相邻梁段连接成整体,如图4(e)所示,全梁共5个螺栓接头。视整段梁所有跨中螺栓全部紧固为健康基准状态,而通过松动某基本周期单元跨中接头螺栓以降低接头刚度,进而模拟该周期单元的损伤状态。该周期铝梁的具体几何与材料参数由表1给出。
本文采用的实验装置系统如图5所示,其主要由实验梁模型、IEPE型加速度计(KT—1000LC)、测试导线、八通道信号采集卡(MPS-140801)、冲击力锤、笔记本电脑以及基于LabVIEw编程的信号采集软件所构成,该软件能实现加速度信号的实时显示、回放以及存储等基本功能。加速度传感器布置在距每跨梁段中部接头6cm处,全梁共布设5个,整体与局部布置方式分别如图5(a)与图5(b)所示。通过冲击力锤对周期梁施加竖向冲击荷载,其作用点距离第一跨右支撑15cm处,如圖5(c)所示。本实验采样频率设为500Hz,以满足采样定理,且每次采样时长约为10s,以包含完整的自由响应信号时间段,实验模态参数识别利用采集的自由响应数据基于自编ERA算法实现。
本次实验共考虑了两种损伤工况,每种工况均有5个待识别损伤参数,即△θ={△θ1,△θ2,…,△θ25}T,分别对应各梁跨的整体刚度降低率。其中,第一种工况仅松动第4号周期梁段跨中铝质夹片的部分螺栓,为单损伤工况;第二种为双损伤工况,其在前一工况基础上进一步松动第5号周期梁段跨中接头的部分螺栓,即此工况下第4,5号周期梁段同时发生损伤。应该指出,本文针对周期支撑梁结构所提出的损伤识别方法其识别对象为各跨梁段的整体刚度降低,因此,本实验通过调整部分周期梁段接头螺栓松紧而造成的梁段跨中局部刚度降低程度,在本文方法框架内将通过其导致的梁段整体刚度降低来反映。
通过重复模态试验,分别获得周期结构健康状态及各损伤工况下的前3阶固有频率各10组,如图6所示,即Nt=3,Ns=10。从图中可以明显看出,频域区间被此3阶模态分成3条明显的条带,各频带内各状态下重复测量所得的模态频率值波动很小,测量结果较稳定。具体地,工况1所设置的损伤对结构第2阶固有频率基本无影响,而对于第3阶模态的影响也较小,相比之下,工况2所对应损伤情况对于后两阶模态频率都有相对明显影响。同时,两种损伤工况对第1阶固有频率影响都较明显,尤其是工况2。此外,为定量反映各损伤情况下模态频率的大小及变化程度,表2给出各工况下重复测量获得的前3阶固有频率均值及变异系数(COV)结果。可以看出,该表给出结果与图6体现的规律相符,同时也反映本次模态试验获得的相关固有频率实测结果的不确定性程度较低。
基于获得的模态试验数据,采用MCMC方法进行损伤参数AO的后验分布采样,先验分布取为零均值高斯分布,模拟次数NMC设为6×104,且取后半部分稳定样本进行参数估计。以工况1为例,图7和图8分别表示各未知参数后验分布样本的散点图矩阵与采样历程。其中,图7中给出的散点图矩阵为散点图的高维扩展,一定程度上克服了在平面上展示高维数据的困难,直观反映出各损伤参数之间的相关性,如△θ1与△θ5,以及△θ2与△θ4之间具有较明显的线性正相关性。实事上,固有频率作为结构整体参数,其对结构对称位置的损伤判定存在困难。尽管本文五跨周期支撑梁实验模型左端边界固定,但整体结构仍保留有一定程度的对称性特征,而给△θ1与△θ5(或△θ2与△θ4)的同时识别带来一定困难。此外,从图8可以明显看出,MCMC模拟中各参数收敛情况较好,且处于周期梁结构中间位置的第3跨损伤参数△θ3的样本波动较大,反映其后验估计的不确定性程度较大。
事实上,本文提出的损伤概率判定条件(即式(37))建立在未知损伤参数后验样本近似服从正态分布基础之上,因而图9以工况1为例对MCMC后验样本的正态分布特征进行检验。该图表示通过MCMC方法采样获得的未知参数后验分布样本的正态分布概率校验图,其很明显地反映各参数后验分布稳定样本点绝大部分落在各条斜直线上,表明各未知参数的穩定后验样本服从正态分布。同时,也可以明显看出损伤参数A03样本斜率大于其余参数,表明该参数后验估计的不确定性较其余未知参数大,与图8中的现象吻合,工况2所得规律与工况1类似。
图10表示两工况下通过MCMC方法抽样获得的各损伤参数后验样本的统计直方图与相应正态分布拟合曲线,该图进一步表明损伤参数的稳定后验样本服从正态分布,这与图9给出的概率分布校验结果相符。同时,从图10中也可以看出两种工况下损伤参数A03后验分布的标准差较其他参数大,而其余参数不确定性程度比较接近,这与此前获得结论相一致。此外,依式(19),(24)以及(25)可知,本文各周期梁段损伤参数△θj(j=1,2,…,N,N=5)识别结果大于0即认为该参数对应梁段理论上发生损伤。对于工况1,图10(a)反映出损伤参数△θ4后验样本均值相对于其余参数明显大于0,这表明第4号梁段整体上很可能发生刚度降低。工况2结果类似,图10(b)表明损伤参数△θ4与△θ5所对应梁段发生整体刚度损失的可能性较大。
应该指出,图10给出结果从均值角度反映出各工况下的实际损伤部位与其近似损伤程度,但其判定是以0为基准。从概率论与数理统计理论上看,以0作为损伤与否的判定基准其可靠性值得商榷。针对该问题,本文设置在给定域内变化的损伤程度阈值d,计算损伤参数的最可能识别值超过该阈值的概率,以合理反映不同阈值下的损伤发生概率,其计算结果如图11所示。从该图中可以明显看出,两种工况下对应于不同损伤程度阈值的各损伤参数以损伤出现的概率大小表征,且损伤概率随损伤程度阈值增加而逐渐降低。同时,工况1中实际发生损伤的第4号周期单元(对应损伤参数△θ4)与工况2中实际发生损伤的第4,5号周期单元(对应损伤参数△θ4与△θ5)在不同损伤程度阈值下均被明显揭示,此损伤判别结果更具合理性。
3结论
提出了一种针对大型周期支撑结构的动力损伤识别有效方法。基于特征波导纳原理与敏感性分析方法,建立有限长周期支撑结构无量纲自振频率敏感性矩阵的一般形式,并结合贝叶斯理论与MCMC模拟方法实现概率损伤识别,以周期支撑梁实验室模型试验对本文方法进行验证。研究结果表明,利用周期支撑结构的固有周期特性,提出的无量纲自振频率及推导的相应敏感性矩阵仅与周期单元总数和结构损伤所处单元位置有关,而与周期结构其他几何材料参数无关,极大地简化了复杂周期支撑结构频率敏感性分析过程,同时也避免了实际应用中损伤敏感性分析计算对于结构准确模型参数的依赖,显著提高了本文损伤识别方法的有效性与实用性。通过设置损伤阈值,本文基于贝叶斯理论的识别方法能给出各单元发生损伤的概率,提高了损伤识别结果评估的合理性与可靠性。本文针对周期支撑梁结构提出的损伤识别方法的识别对象为各跨梁段的整体刚度降低,因而,在本文方法框架内,本次实验通过调整周期梁段接头螺栓松紧而造成的梁段跨中局部刚度改变程度,是通过其引起的梁段整体刚度降低程度来反映。

