不同应力比下疲劳裂纹扩展行为研究

2023.02.15

李杨杨莹汪舟

摘要：以扩展有限单元法（extended finite element method，XFEM）为理论基础，研究了不同应力比（R=0.02，0.1，0.2，04）对含初始预制裂纹的Q235钢紧凑拉伸试件（compact tension，CT）疲劳裂纹扩展行为的影响，并设计了对应的试验加以验证。结果表明：最大载荷Pmax和应力比R不变时，疲劳裂纹扩展速率随着裂纹扩展长度曾加而逐渐增大;在相同最大载荷Pmax下，试件疲劳裂纹扩展到20mm所需要的循环次数N随应力比R的增大而增大;在相同应力比R下，试件疲劳裂纹扩展到20mm所需要的循环次数N随最大载荷的增大而减少。

关键词：XFEM;CT试件;应力比;疲劳裂纹扩展

随着汽车轻量化的不断深入，材料疲劳成为引发汽车零部件失效的主要因素[1]。20世纪90年代末，基于有限元和断裂力学理论发展的扩展有限元法诞生，它是为了解决复杂断裂问题而提出的一种新的方法[2]。Belytsehko[3]首先提出采用独立于有限元网格的扩展有限元来求解裂纹等间断问题，该思想主要来源于单位分解法[4]，该方法被认为是扩展有限元法的前身。随后，Moes[5]等将扩充函数引入到裂纹扩展的计算函数中，为研究断裂力学提供了一种新的方法，最终被定义为扩展有限元法。金属结构或者构件在循环应力或应变的扰动下，在一处或者多处位置会产生损伤累积效应，经过一定循环次数后会产生永久性的损伤，如产生微裂纹。虽然材料应力值始终没有超过材料的强度极限，甚至比材料的弹性极限还小的情况下，疲劳微裂纹仍然会随着循环次数的增加而发生扩展现象，在这种交变载荷作用下最终发生疲劳断裂。根据上述疲劳裂纹扩展特点可以进行如下划分：首先裂纹在结构的应力集中区域成核（Ⅰ区），在该区内疲劳裂纹扩展我们认为有一个门槛值△Kth，当疲劳裂纹尖端的应力强度因子幅值△Kth小于疲劳裂纹扩展的门槛值△Kth时，疲劳裂纹将不会发生扩展或者疲劳裂纹扩展的速率极其缓慢;然后疲劳裂纹扩展长度和循环次数基本成正比关系（Ⅱ区），并且满足Paris公式，其中da/dN和△K在对数坐标系下接近一条直线，此阶段裂纹扩展规律性最明显，是研究的热点区域;最后疲劳裂纹扩展速率将急速增大（Ⅲ区），结构或构件将很快发生破坏或断裂，此阶段的疲劳寿命在三个阶段是最小的。

本文基于扩展有限单元法选取了工程上常用的Q235钢CT试件为研究对象，对其XFEM裂纹扩展进行了数值模拟，探究了应力比和载荷对疲劳裂纹扩展速率的影响。

一、XFEM疲劳裂纹数值模拟

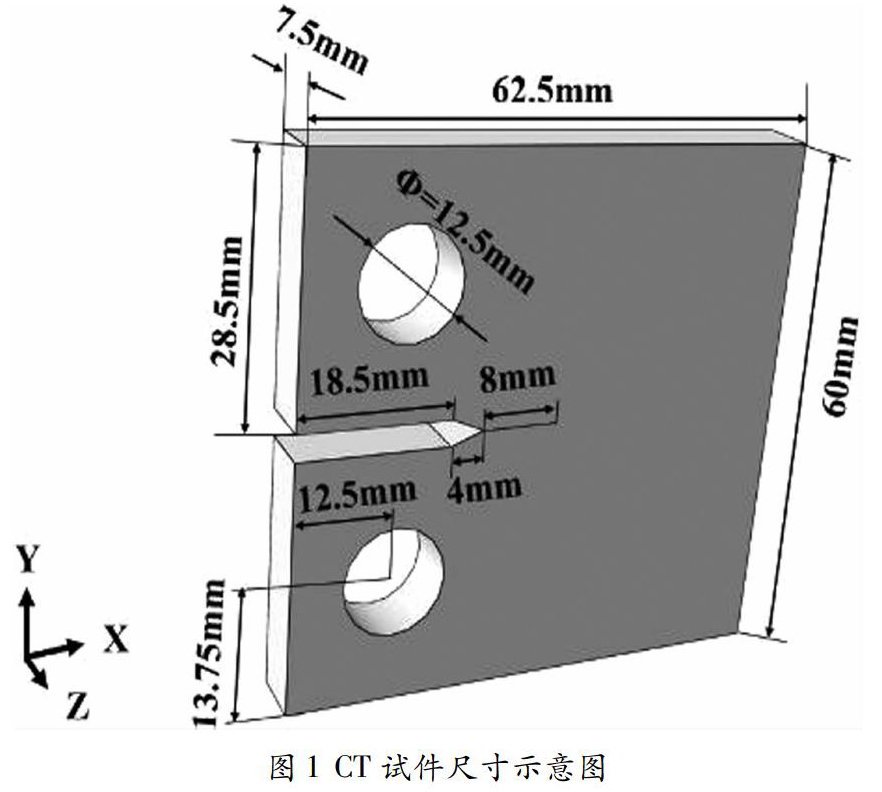
根据美国材料与试验协会ASTME647-95a和国家GB/T 6398-2017关于金属疲劳试验和疲劳裂纹扩展方法的标准，选取CT试件作为疲劳裂纹扩展研究对象。CT试样的基本参数为厚度B=7.5mm，从加载孔中心面到试样右边缘的距离W=50mm，其中加载孔直径D=12.5mm，中间前端楔形区域包括长为18.5mm，高为3mm的矩形区域和底为3mm，高为4mm的等腰三角形。中间前端楔形区域紧接着预制一条长度为8mm的高精度线切割裂纹，材料选用Q235钢，弹性模量为2.06×1011，泊松比为0.28。具体参数见表1，试件三维模型尺寸见图1。

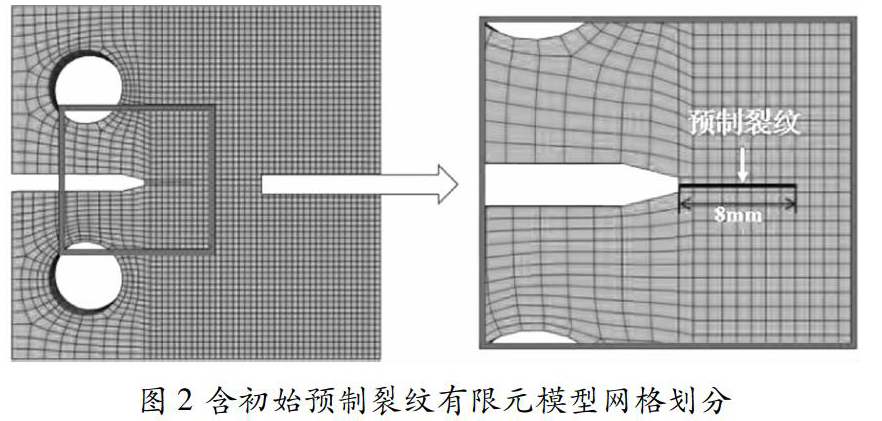
创建CT试件有限元模型，并定义材料属性。损伤起始准则为最大主应力准则，计算损伤演化采用能量线性软化和幂法则混合的方式，并设三向断裂都相等，并在.inp文件中相互作用属性关键字中添加疲劳参数，最大主应力设为235MPa，幂指数设为1.0，断裂能设为42200N/m;预制裂纹面定义为XFEM裂纹，并创建一个硬接触属性;网格划分如图2所示，为了后期减少模型计算成本、提高计算精度及方便测量裂纹扩展的长度，可以进行部分区域的网格细化，在模型左右上下相关边界布置对称种子并使网格大小为1mm，由XFEM理论可知当裂纹在单元内部和穿过单元时并不会降低计算的准确性且由有限元仿真模拟结果可知，当裂纹预制在单元内部时，扩展效果反而更好。整体模型网格采用C3D8R（8节点六面体线形减缩积分）单元划分，共得到17820个C3D8R单元，见图2。

在ABAQUS中，创建一个直接循环分析步（Direct cyclic），0.2作为循环周期，采用固定式增量步，500000为增量步的极限值，0.02为增量步的大小，设100为最大迭代数的极限值，设25为傅里叶级数的初始项，20为增量大小，幅值函数循环增量步极限值分别为1和10，根据疲劳试验数据，加载循环次数的极限值为100000;场变量输出节点XFEM水平集函数PHILSM、PSILSM、和节点位移，历程变量输出疲劳加载的循环次数、XFEM单元状态、单元应力及应变;在Load模块中上耦合点的集中力分别设置Y方向6000N集中力并在Amplitude中創建幅值函数，分别创建应力比R=0.1的幅值曲线函数的参数条件。分别记录下裂纹每扩展1mm需要的循环次数，记录到裂纹扩展长度为20mm停止。

二、应力比和载荷对疲劳裂纹扩展速率的影响

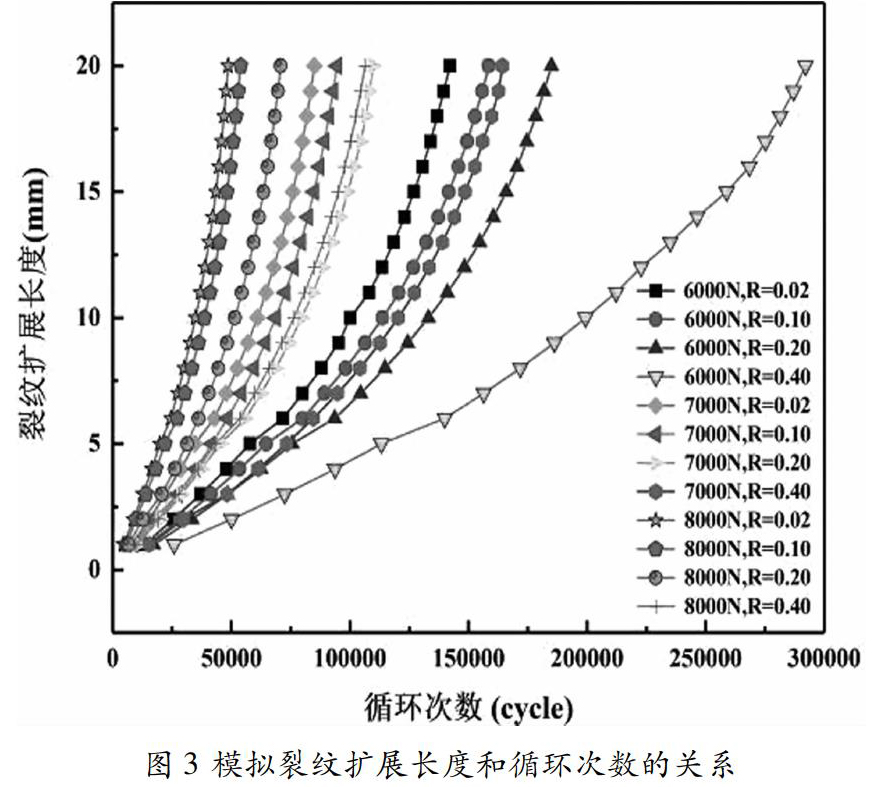
使用ABAQUS软件XFEM分别对参数不同的12个CT试件有限元模型进行模拟，然后分别记录裂纹每扩展1mm所需要的循环次数，便可得到应力比和最大加载幅值下疲劳裂纹扩展的长度与循环次数的关系，如图3所示。

为了更加直观地得到疲劳裂纹扩展速率和循环次数的关系，故采用割线法对图3中的数据点进行处理。分别计算裂纹在每发生1mm长度内疲劳裂纹扩展速率da/dN的平均值来代表该1mm起始时的疲劳裂纹扩展速率，然后得到疲劳裂纹扩展速率和循环次数的关系图，见图4。

分析图3及图4可知：在相同最大载荷Pmax下，试件疲劳裂纹扩展到20mm所需要的循环次数N随应力比R的增大而增大，以6000N、R=0.02、N=142100为基准：R=0.10时N=158570，增幅为11.59%;R=0.20时N=184940，增幅为30.15%;R=0.40时N=272130，增幅为47.78%。在相同应力比R下，试件疲劳裂纹扩展到20mm所需要的循环次数N随最大载荷的增大而减少，以Pmax=6000N、R=0.1、N=158570为基准：Pmax=7000N时N=94555，降幅为40.37%;Pmax=8000N时N=53962，降幅为65.97%。综上，应力比R和最大载荷Pmax都会对裂纹扩展寿命产生较大影响。

三、结论

本文以扩展有限单元法为仿真理论基础，并以CT试件为研究对象，分别对不同应力比R下疲劳裂纹扩展进行了模拟及试验验证，最大载荷Pmax和应力比R不变时，疲劳裂纹扩展速率随着裂纹扩展长度曾加而逐渐增大;在相同最大载荷Pmax下，试件疲劳裂纹扩展到20mm所需要的循环次数N随应力比R的增大而增大;在相同应力比R下，试件疲劳裂纹扩展到20mm所需要的循环次数N随最大载荷的增大而减少。

参考文献：

[1]陈传尧.疲劳与断裂[M].武汉：华中科技大学出版社，2002.

[2]庄茁，柳占立，成彬彬，等.扩展有限单元法[M].北京：清华大学出版社，2012.

[3]Belytsehko T，Blaek T.Elastic crack growth in finite elements with minimal remeshing[J].International Journal for numerical Methods in Engineering，1999，45（5）：601-620.

[4]Melenk J M，Babuska I.The Partition of Unity Finite Element Method：Basic Theory and Applications[J].Computer methods in applied mechanics and engineering，1996，139（1-4）：289-314.

[5]Moes N，Dolbow J，Belytschko T.A finite element method for crack growth without remeshing[J].International journal for Numerical Methods in Engineering，1999，46（1）：131-150.

作者简介：李杨（1995—），男，河北衡水人，硕士，研究方向：汽车轻量化。