考虑CSI效应的AMD控制系统构建及其时变时滞补偿
陈朝骏 李祚华 滕军 幸厚冰


摘要:由于AMD控制系统与结构之间存在着相互作用CSI(control-structureinteraction),造成了以惯性质量为支撑点向被控结构施加的控制力不等于理论的最优控制力,即施加的控制力将有所滞后。为此,针对AMD控制系统建立了不计CSI效应、计低阶CSI效应和同时计低、高阶CSI效应的三种数学模型,经分析表明了计低、高阶CSI效应对AMD控制系统的影响最大,进而确定了由CSI效应造成的时变时滞的范围。针对某4层钢框架实验系统,基于保性能算法设计了相应的时变时滞补偿控制器,以系统控制效果、AMD控制力及行程为指标,对比了有无时滞的两种控制系统的性能,结果表明在较大的时变时滞的影响下,此控制算法依旧具有良好的控制效果以及稳定的控制参数。关键词:振动控制;高柔结构;AMD控制系统;时变时滞;保性能控制
中图分类号:TU352.2;TU973.2 文献标志码:A 文章编号:1004-4523(2018)01-0020-10
DOI:10.16385/j.cnki.issn.1004-4523.2018.01.003
引言
高柔结构的主动质量阻尼器AMD(activemassdamper)具有控制效果好、控制频带宽等优点,多用于控制该结构水平方向的动力响应。由于AMD控制系统存在着时滞效应,导致了系统性能的降低甚至失稳,限制了AMD控制系统的发展以及运用。
时滞主要来源于数据采集时滞、控制力计算时滞以及执行机构响应时滞等。其中,数据采集时滞较小,可不考虑其影响;对于控制力计算时滞,目前已有学者提出了考虑高阶振型信息的低维控制器设计方法,该方法压缩了计算量,降低了控制力计算时滞对系统的影响。实际AMD控制系统的执行机构响应时滞主要受控制器与结构间的相互作用CSI(control-structure interaction)的影响。在实际工程中,Stewart等对比分析了应用于风轮机的主动控制系统中考虑与不考虑CSI效应的影响,结果表明考虑CSI效应的控制系统控制效果更好。执行机构的灵敏度在很大程度上取决于驱动形式,本文所采用的电磁驱动AMD系统是最为常见的一种控制方式。除此之外,目前有关控制系统CSI效应影响侧重于CSI效应对系统控制效果的影响。但在实际工程中,反馈信号的输入频率将对CSI效应造成影响,可通过分析寻求合适的控制电压输入频率以减弱CSI效应的影响。同时,由于该输入频率时刻在变化,该部分时滞是时变性也是不可忽略的。
由于时变时滞的影响,LQR控制器往往不能保证闭环系统的稳定性及期望性能。因此需要对系统的时滞进行相应的补偿。实际中,Xu等针对不确定时滞系统提出了非脆弱鲁棒H∞控制器设计方法。H∞控制主要考虑了系统的鲁棒稳定性,牺牲了系统的性能,而保性能控制算法GCC(guaranteed cost control)是一种将系统性能和鲁棒性相结合的LQR控制器设计方法。为了成功地将GCC算法运用到高柔结构中,在对时滞系统进行保性能状态反馈控制器的设计之前,需要求解Riccati矩阵方程的正定解,早期主要基于Riccati方程的方法,但这种方法需人为事先确定某些待定参数,然而当前依旧缺乏寻找这些参数的最优值的方法,这类人为确定参数的方法给控制系统带来了很大的保守性,并且求解Riccati方程的方法多为迭代方法,其收敛性不能得到保证,而线性矩阵不等式LMI(Linear matrix inequality)方法可以克服求解Riccati方程困难的问题。因此,针对CSI效应产生的时变时滞,研究基于LMI的保性能状态反馈时变时滞补偿控制器设计方法更有实际意义。
綜上分析,本文先以4层钢框架结构为分析对象,建立了该结构AMD系统的不计CSI效应、计低阶CSI效应和同时计低、高阶CSI效应时的数学模型,分析了控制电压输入频率对CSI效应的影响。再针对时变时滞系统,提出了保性能时滞补偿控制增益的设计方法,将该系统的增益求解问题表示为非线性矩阵不等式组,并通过变量替换法转化为易求解的线性矩阵不等式组,再由LMI工具箱求解出最优解。最后通过与无时滞系统进行对比,验证了保性能时滞补偿增益的有效性。
1考虑CSI的AMD控制系统
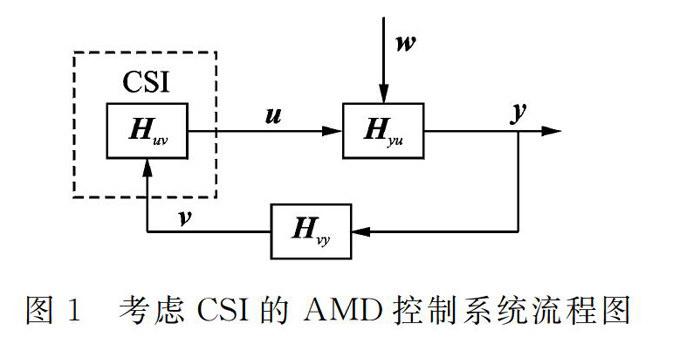
AMD控制系统的流程可由图1简单描述。图中,v为控制电压(或电流)信号,u为控制力,w为外激励荷载,Huv为伺服电机控制电压(或电流)到控制力的传递函数,Hyu为控制力到被控结构响应的传递函数,Hvy为反馈状态到控制电压(或电流)的传递函数。控制器与结构间的相互作用是指AMD控制系统中控制器与结构间的相互动力影响即CSI效应,如图1中虚线框表示。
若考虑外激励作用,控制系统的力平衡方程为
将控制力与外激励分开考虑,式(1)可写成状态方程为
目前以电磁驱动的AMD系统应用最为常见,驱动形式在很大程度上决定了执行机构的灵敏度。若控制系统的执行机构反应足够灵敏,则可在该周期内完成最优控制力的施加,即系统的执行机构响应时滞较小。然而在实际工程中,执行机构响应滞后致使最优控制力施加滞后,可见CSI效应其实是表现为控制系统的控制时滞。
以常用于土木结构控制领域中的永磁直流(DC)旋转电动机为例,如图2所示。该类型电机的具体参数参考了文献,对应的输入输出关系可由下式表示
系统驱动力为
从式(6)可看出,控制力受到了结构顶层相对速度的影响,说明由于CSI的影响,使得结构与AMD控制系统的性能是结合在一起的。而且,式(6)还包含了控制力的高阶项。因此根据不同精度解的要求,以某一单自由度AMD控制系统为例,其参数如表1所示,针对上述伺服电机参数建立了该系统不计CSI效应、计低阶CSI效应和同时计低、高阶CSI效应三类不同情况的数学模型,如图3所示。当不考虑CSI效应,系统的控制力与电压间成线性关系,即仅考虑图3中的(a)项,此时系统为理想系统;当AMD控制系统的驱动力变化率为零,即不考虑图3中的(c)项时,此时系统仅考虑了低阶CSI效应;当系统驱动力变化率不为零,即同时考虑图3中的(a),(b)和(c)项,此时系统考虑了低、高阶CSI效应。
1.1不计CSI效应
不计CSI效应时,系统的控制力与控制电压间的关系为
系统的状态方程为
系统的输出方程为
在Matlab软件Simulink仿真工具箱的环境下,根据式(11)和(12),建立了不计CSI效应的数学模型。从式(12)可得,系统的输出包括了位移、速度、加速度及控制力。此时,再利用命令“Bode”函数绘制出控制电压到控制力的传递函数,其中输入为控制电压、输出为控制力,其幅值及相角如图4所示。司以看出:(1)传递函数的幅值为一常数,即输出(控制力)与输入(控制电压)成线性关系;(2)传递函数的相角差恒为零,即控制力与控制电压保持同相位,说明此时控制电压到控制力的转化过程无时间滞后。
1.2计低阶CSI效应
仅考虑低阶CSI效应时,伺服电机的输入输出关系为
同理,根据式(14)和(15),建立了仅计低阶CSI效应的数学模型。此时,其控制电压到控制力的传递函数的幅值及相角如图5所示。可以看出:(1)随着控制电压输入频率的增大,传递函数的幅值逐渐增大,而相角差逐渐增大(相角差为负值表明控制力滞后于控制电压),最后均趋近于零,说明输入电压到输出控制力的转换时滞随控制电压输入频率的增大而逐渐减小,而幅值逐渐增大;(2)计及低阶CSI效应时,控制力与控制电压间的关系受控制电压输入频率的影响,而不再保持线性关系。
1.3同时计低、高阶CSI效应
同时计低、高阶CSI效应的控制系统,伺服电机的输入输出关系为
系统的状态方程为
最后,根据式(17)和(18)建立了同时计低、高阶CSI效应的数学模型。此时,其控制电压到控制力的传递函数的幅值及相角如图6所示。可以看出:(1)随着控制电压输入频率的增大,传递函数的幅值和相角差均先增大后减小;(2)当控制电压输入频率过大或过小时,其到控制力传递函数幅值及相角差较小,说明此时单位控制电压对应的控制力较小,且时间滞后较大。
综合图4~6可知:(1)理想情况下AMD控制系统的输入到输出传递函数的幅值最大,即单位控制电压产生的控制力最大,而相角差相比最小,即控制力滞后于控制电压的时间最短。因此,不计CSI效应的伺服电机性能相比最好,计及低阶CSI效应时次之,而计及高阶CSI效应时最差;(2)外激励(包括控制力)的频率过大或过小时,传递函数幅值及相角(负值)较小,则单位电压产生的控制力较小,且控制力滞后于控制电压的时间较长,即控制系统的时滞较大;若适当减小(或增大)控制力输出频率使得其位于幅频曲线和相频曲线的峰值附近,则单位控制电压可转换成较大的控制力且控制系统附加时滞会较小;(3)外界激励对AMD控制系统影响,也可归结为对控制电压到控制力传递函数的幅值(影响控制力大小,与控制增益对应)或相角(影响控制力相位,与控制时滞对应)的影响。因为AMD控制系统持续对被控结构施加控制力,系统受外界的影响可主要是对传递函数相角的影响。
2实验系统的时滞范围确定
由图4~6可知,当控制力的频率一定,则控制输入到输出的相角差一定,即控制输出滞后于输入的延时一定;而当控制力(包括外激励)的频率时刻变化时,系统的时滞将时刻变化。以El Centro波(SN向)为例,其调幅后的时程曲线及其经FFT变换之后的付氏谱特性曲线如图7所示,此时地震波作用下不计CSI效应、计低阶CSI效应和同时计低、高阶CSI效应的系统控制电压与控制力归一化后的对比情况如图8所示。可知,在El Centro波作用下,不计CSI效应及计低阶CSI效应时控制力与控制电压基本同步,而同时计低、高阶CSI效应时系统控制力滞后于控制电压较多,此种情况与实际工程最为接近,故实际中控制力滞后于控制电压一个时变时滞。
上述伺服电机控制系统控制力滞后于控制电压的时滞随时间变化曲线及其变化率曲线如图9所示。可以看出:(1)El Centro波作用下,上述伺服控制系统控制力滞后于控制电压的时间变化较大,其最大时滞为0.11s;(2)地震作用结束后,控制力滞后于控制电压的时间保持常数(0.11s)且达到最大。这是由于此时外激励频率(或反馈信号频率,即控制电压输入频率)为0,相角差最大,则控制系统的时滞最大。
3保性能时滞补偿控制器设计
3.1保性能时滞补偿增益设计原理
由于频率不一的外激励作用下,同时计低、高阶CSI效应时伺服电机的输入(控制电压)到输出(控制力)存在着较大的时变时滞。因此,进行保性能时滞补偿控制增益的设计尤为必要。
受时滞影响的系统控制力为(19)式中G为控制系统的保性能时滞补偿增益,d(t)为控制系统的时滞。
将式(19)代入式(2),若不考虑外激励作用,则系统状态方程为
在外激励及控制力作用下,考虑时滞影响的闭环系统可表示为
(27)则系统(25)是渐近稳定的。由式(27)可得
对式(29)两边进行积分,可求得时滞闭环系统的性能指标满足
3.2实验结果分析
针对文献[8]所述的实验系统,基于3.1节为理论基础设计该实验系统的最优状态反馈保性能时滞补偿控制器,并通过延迟输出控制力引人大小为0~0.5s的随机时滞。本文重点关注AMD装置所在结构楼层(第4层)的控制效果以及AMD行程的大小。为了能够选取到合适的权系数,本文先设计了该实验系统的LQR经典最优控制器,再通过对该结构各楼层的控制效果以及AMD控制参数进行数值分析,最终确定了权矩阵中第4层位移项、AMD惯性质量块位移项以及经济指标所对应的加权系数Q4,Q5和R的取值,分别为6×105,3×102和1×10-3,其余各层的加权系数均设为零。在加载频率为1Hz,峰值为45.89N的正弦激励荷载作用下,无控、无时滞系统和有时滞且Gcc補偿系统的结构第4层位移、加速度响应对比情况如图10,11所示,对应的结构响应、控制效果以及AMD性能指标如表2所示。表2中的每一工况的实验取时为300s,图10,11中都仅给出时间为30s的数据。
从图10,11及表2可以看出:(1)当不考虑时滞效应时,本文设计的最优状态反馈保性能控制器能有效地控制结构响应;(2)当考虑时滞效应时,该控制器还可对时变时滞进行补偿,保性能控制器依然有效,结构位移、加速度控制效果较无时滞系统而言,分别仅变化了4.15%,-5.58%;因此,运用保性能控制方法对AMD控制系统中含有较大时变时滞的工况时,依然能够将结构响应控制在较理想的范围内。
4结论
本文基于伺服电机输入输出关系建立了4层钢框架AMD控制系统3种不同类型的CSI效应的数学模型,明确了CSI效应对控制系统的影响主要表现为造成了系统时滞的时变性,进而分析了该时变时滞的范围,最后设计了相应的保性能时变时滞补偿控制器。得出主要结论如下:
(1)当AMD控制系统不考虑CSI效应时,控制电压到控制力传递函数的幅值为定值,而其相角为零,控制系统的附加时滞为零。
(2)当AMD控制系统考虑CSI效应时,可通过适当调节控制电压输入频率(控制力输出频率),使得其位于幅频曲线和相频曲线的峰值附近,此时传递函数的幅值最大而相角最小,即单位控制电压可转换成较大的控制力且控制系统的附加时滞会较小。
(3)AMD控制系统的CSI效应其实质为控制力滞后于控制电压的时间。在频率不一的外激励如地震荷载的作用下,该时滞为某一时刻变化的量,因此实际AMD控制系统为时变时滞控制系统。
(4)当系统考虑时变时滞时,最优状态反馈保性能控制器能明显减轻结构的风振响应,且与无时滞系统相比,两者的控制效果、AMD控制力及其行程输出基本相当。因此,本文设计的最优状态反馈保性能时滞补偿控制器能有效减小CSI效应的影响。



摘要:由于AMD控制系统与结构之间存在着相互作用CSI(control-structureinteraction),造成了以惯性质量为支撑点向被控结构施加的控制力不等于理论的最优控制力,即施加的控制力将有所滞后。为此,针对AMD控制系统建立了不计CSI效应、计低阶CSI效应和同时计低、高阶CSI效应的三种数学模型,经分析表明了计低、高阶CSI效应对AMD控制系统的影响最大,进而确定了由CSI效应造成的时变时滞的范围。针对某4层钢框架实验系统,基于保性能算法设计了相应的时变时滞补偿控制器,以系统控制效果、AMD控制力及行程为指标,对比了有无时滞的两种控制系统的性能,结果表明在较大的时变时滞的影响下,此控制算法依旧具有良好的控制效果以及稳定的控制参数。关键词:振动控制;高柔结构;AMD控制系统;时变时滞;保性能控制
中图分类号:TU352.2;TU973.2 文献标志码:A 文章编号:1004-4523(2018)01-0020-10
DOI:10.16385/j.cnki.issn.1004-4523.2018.01.003
引言
高柔结构的主动质量阻尼器AMD(activemassdamper)具有控制效果好、控制频带宽等优点,多用于控制该结构水平方向的动力响应。由于AMD控制系统存在着时滞效应,导致了系统性能的降低甚至失稳,限制了AMD控制系统的发展以及运用。
时滞主要来源于数据采集时滞、控制力计算时滞以及执行机构响应时滞等。其中,数据采集时滞较小,可不考虑其影响;对于控制力计算时滞,目前已有学者提出了考虑高阶振型信息的低维控制器设计方法,该方法压缩了计算量,降低了控制力计算时滞对系统的影响。实际AMD控制系统的执行机构响应时滞主要受控制器与结构间的相互作用CSI(control-structure interaction)的影响。在实际工程中,Stewart等对比分析了应用于风轮机的主动控制系统中考虑与不考虑CSI效应的影响,结果表明考虑CSI效应的控制系统控制效果更好。执行机构的灵敏度在很大程度上取决于驱动形式,本文所采用的电磁驱动AMD系统是最为常见的一种控制方式。除此之外,目前有关控制系统CSI效应影响侧重于CSI效应对系统控制效果的影响。但在实际工程中,反馈信号的输入频率将对CSI效应造成影响,可通过分析寻求合适的控制电压输入频率以减弱CSI效应的影响。同时,由于该输入频率时刻在变化,该部分时滞是时变性也是不可忽略的。
由于时变时滞的影响,LQR控制器往往不能保证闭环系统的稳定性及期望性能。因此需要对系统的时滞进行相应的补偿。实际中,Xu等针对不确定时滞系统提出了非脆弱鲁棒H∞控制器设计方法。H∞控制主要考虑了系统的鲁棒稳定性,牺牲了系统的性能,而保性能控制算法GCC(guaranteed cost control)是一种将系统性能和鲁棒性相结合的LQR控制器设计方法。为了成功地将GCC算法运用到高柔结构中,在对时滞系统进行保性能状态反馈控制器的设计之前,需要求解Riccati矩阵方程的正定解,早期主要基于Riccati方程的方法,但这种方法需人为事先确定某些待定参数,然而当前依旧缺乏寻找这些参数的最优值的方法,这类人为确定参数的方法给控制系统带来了很大的保守性,并且求解Riccati方程的方法多为迭代方法,其收敛性不能得到保证,而线性矩阵不等式LMI(Linear matrix inequality)方法可以克服求解Riccati方程困难的问题。因此,针对CSI效应产生的时变时滞,研究基于LMI的保性能状态反馈时变时滞补偿控制器设计方法更有实际意义。
綜上分析,本文先以4层钢框架结构为分析对象,建立了该结构AMD系统的不计CSI效应、计低阶CSI效应和同时计低、高阶CSI效应时的数学模型,分析了控制电压输入频率对CSI效应的影响。再针对时变时滞系统,提出了保性能时滞补偿控制增益的设计方法,将该系统的增益求解问题表示为非线性矩阵不等式组,并通过变量替换法转化为易求解的线性矩阵不等式组,再由LMI工具箱求解出最优解。最后通过与无时滞系统进行对比,验证了保性能时滞补偿增益的有效性。
1考虑CSI的AMD控制系统
AMD控制系统的流程可由图1简单描述。图中,v为控制电压(或电流)信号,u为控制力,w为外激励荷载,Huv为伺服电机控制电压(或电流)到控制力的传递函数,Hyu为控制力到被控结构响应的传递函数,Hvy为反馈状态到控制电压(或电流)的传递函数。控制器与结构间的相互作用是指AMD控制系统中控制器与结构间的相互动力影响即CSI效应,如图1中虚线框表示。
若考虑外激励作用,控制系统的力平衡方程为
将控制力与外激励分开考虑,式(1)可写成状态方程为
目前以电磁驱动的AMD系统应用最为常见,驱动形式在很大程度上决定了执行机构的灵敏度。若控制系统的执行机构反应足够灵敏,则可在该周期内完成最优控制力的施加,即系统的执行机构响应时滞较小。然而在实际工程中,执行机构响应滞后致使最优控制力施加滞后,可见CSI效应其实是表现为控制系统的控制时滞。
以常用于土木结构控制领域中的永磁直流(DC)旋转电动机为例,如图2所示。该类型电机的具体参数参考了文献,对应的输入输出关系可由下式表示
系统驱动力为
从式(6)可看出,控制力受到了结构顶层相对速度的影响,说明由于CSI的影响,使得结构与AMD控制系统的性能是结合在一起的。而且,式(6)还包含了控制力的高阶项。因此根据不同精度解的要求,以某一单自由度AMD控制系统为例,其参数如表1所示,针对上述伺服电机参数建立了该系统不计CSI效应、计低阶CSI效应和同时计低、高阶CSI效应三类不同情况的数学模型,如图3所示。当不考虑CSI效应,系统的控制力与电压间成线性关系,即仅考虑图3中的(a)项,此时系统为理想系统;当AMD控制系统的驱动力变化率为零,即不考虑图3中的(c)项时,此时系统仅考虑了低阶CSI效应;当系统驱动力变化率不为零,即同时考虑图3中的(a),(b)和(c)项,此时系统考虑了低、高阶CSI效应。
1.1不计CSI效应
不计CSI效应时,系统的控制力与控制电压间的关系为
系统的状态方程为
系统的输出方程为
在Matlab软件Simulink仿真工具箱的环境下,根据式(11)和(12),建立了不计CSI效应的数学模型。从式(12)可得,系统的输出包括了位移、速度、加速度及控制力。此时,再利用命令“Bode”函数绘制出控制电压到控制力的传递函数,其中输入为控制电压、输出为控制力,其幅值及相角如图4所示。司以看出:(1)传递函数的幅值为一常数,即输出(控制力)与输入(控制电压)成线性关系;(2)传递函数的相角差恒为零,即控制力与控制电压保持同相位,说明此时控制电压到控制力的转化过程无时间滞后。
1.2计低阶CSI效应
仅考虑低阶CSI效应时,伺服电机的输入输出关系为
同理,根据式(14)和(15),建立了仅计低阶CSI效应的数学模型。此时,其控制电压到控制力的传递函数的幅值及相角如图5所示。可以看出:(1)随着控制电压输入频率的增大,传递函数的幅值逐渐增大,而相角差逐渐增大(相角差为负值表明控制力滞后于控制电压),最后均趋近于零,说明输入电压到输出控制力的转换时滞随控制电压输入频率的增大而逐渐减小,而幅值逐渐增大;(2)计及低阶CSI效应时,控制力与控制电压间的关系受控制电压输入频率的影响,而不再保持线性关系。
1.3同时计低、高阶CSI效应
同时计低、高阶CSI效应的控制系统,伺服电机的输入输出关系为
系统的状态方程为
最后,根据式(17)和(18)建立了同时计低、高阶CSI效应的数学模型。此时,其控制电压到控制力的传递函数的幅值及相角如图6所示。可以看出:(1)随着控制电压输入频率的增大,传递函数的幅值和相角差均先增大后减小;(2)当控制电压输入频率过大或过小时,其到控制力传递函数幅值及相角差较小,说明此时单位控制电压对应的控制力较小,且时间滞后较大。
综合图4~6可知:(1)理想情况下AMD控制系统的输入到输出传递函数的幅值最大,即单位控制电压产生的控制力最大,而相角差相比最小,即控制力滞后于控制电压的时间最短。因此,不计CSI效应的伺服电机性能相比最好,计及低阶CSI效应时次之,而计及高阶CSI效应时最差;(2)外激励(包括控制力)的频率过大或过小时,传递函数幅值及相角(负值)较小,则单位电压产生的控制力较小,且控制力滞后于控制电压的时间较长,即控制系统的时滞较大;若适当减小(或增大)控制力输出频率使得其位于幅频曲线和相频曲线的峰值附近,则单位控制电压可转换成较大的控制力且控制系统附加时滞会较小;(3)外界激励对AMD控制系统影响,也可归结为对控制电压到控制力传递函数的幅值(影响控制力大小,与控制增益对应)或相角(影响控制力相位,与控制时滞对应)的影响。因为AMD控制系统持续对被控结构施加控制力,系统受外界的影响可主要是对传递函数相角的影响。
2实验系统的时滞范围确定
由图4~6可知,当控制力的频率一定,则控制输入到输出的相角差一定,即控制输出滞后于输入的延时一定;而当控制力(包括外激励)的频率时刻变化时,系统的时滞将时刻变化。以El Centro波(SN向)为例,其调幅后的时程曲线及其经FFT变换之后的付氏谱特性曲线如图7所示,此时地震波作用下不计CSI效应、计低阶CSI效应和同时计低、高阶CSI效应的系统控制电压与控制力归一化后的对比情况如图8所示。可知,在El Centro波作用下,不计CSI效应及计低阶CSI效应时控制力与控制电压基本同步,而同时计低、高阶CSI效应时系统控制力滞后于控制电压较多,此种情况与实际工程最为接近,故实际中控制力滞后于控制电压一个时变时滞。
上述伺服电机控制系统控制力滞后于控制电压的时滞随时间变化曲线及其变化率曲线如图9所示。可以看出:(1)El Centro波作用下,上述伺服控制系统控制力滞后于控制电压的时间变化较大,其最大时滞为0.11s;(2)地震作用结束后,控制力滞后于控制电压的时间保持常数(0.11s)且达到最大。这是由于此时外激励频率(或反馈信号频率,即控制电压输入频率)为0,相角差最大,则控制系统的时滞最大。
3保性能时滞补偿控制器设计
3.1保性能时滞补偿增益设计原理
由于频率不一的外激励作用下,同时计低、高阶CSI效应时伺服电机的输入(控制电压)到输出(控制力)存在着较大的时变时滞。因此,进行保性能时滞补偿控制增益的设计尤为必要。
受时滞影响的系统控制力为(19)式中G为控制系统的保性能时滞补偿增益,d(t)为控制系统的时滞。
将式(19)代入式(2),若不考虑外激励作用,则系统状态方程为
在外激励及控制力作用下,考虑时滞影响的闭环系统可表示为
(27)则系统(25)是渐近稳定的。由式(27)可得
对式(29)两边进行积分,可求得时滞闭环系统的性能指标满足
3.2实验结果分析
针对文献[8]所述的实验系统,基于3.1节为理论基础设计该实验系统的最优状态反馈保性能时滞补偿控制器,并通过延迟输出控制力引人大小为0~0.5s的随机时滞。本文重点关注AMD装置所在结构楼层(第4层)的控制效果以及AMD行程的大小。为了能够选取到合适的权系数,本文先设计了该实验系统的LQR经典最优控制器,再通过对该结构各楼层的控制效果以及AMD控制参数进行数值分析,最终确定了权矩阵中第4层位移项、AMD惯性质量块位移项以及经济指标所对应的加权系数Q4,Q5和R的取值,分别为6×105,3×102和1×10-3,其余各层的加权系数均设为零。在加载频率为1Hz,峰值为45.89N的正弦激励荷载作用下,无控、无时滞系统和有时滞且Gcc補偿系统的结构第4层位移、加速度响应对比情况如图10,11所示,对应的结构响应、控制效果以及AMD性能指标如表2所示。表2中的每一工况的实验取时为300s,图10,11中都仅给出时间为30s的数据。
从图10,11及表2可以看出:(1)当不考虑时滞效应时,本文设计的最优状态反馈保性能控制器能有效地控制结构响应;(2)当考虑时滞效应时,该控制器还可对时变时滞进行补偿,保性能控制器依然有效,结构位移、加速度控制效果较无时滞系统而言,分别仅变化了4.15%,-5.58%;因此,运用保性能控制方法对AMD控制系统中含有较大时变时滞的工况时,依然能够将结构响应控制在较理想的范围内。
4结论
本文基于伺服电机输入输出关系建立了4层钢框架AMD控制系统3种不同类型的CSI效应的数学模型,明确了CSI效应对控制系统的影响主要表现为造成了系统时滞的时变性,进而分析了该时变时滞的范围,最后设计了相应的保性能时变时滞补偿控制器。得出主要结论如下:
(1)当AMD控制系统不考虑CSI效应时,控制电压到控制力传递函数的幅值为定值,而其相角为零,控制系统的附加时滞为零。
(2)当AMD控制系统考虑CSI效应时,可通过适当调节控制电压输入频率(控制力输出频率),使得其位于幅频曲线和相频曲线的峰值附近,此时传递函数的幅值最大而相角最小,即单位控制电压可转换成较大的控制力且控制系统的附加时滞会较小。
(3)AMD控制系统的CSI效应其实质为控制力滞后于控制电压的时间。在频率不一的外激励如地震荷载的作用下,该时滞为某一时刻变化的量,因此实际AMD控制系统为时变时滞控制系统。
(4)当系统考虑时变时滞时,最优状态反馈保性能控制器能明显减轻结构的风振响应,且与无时滞系统相比,两者的控制效果、AMD控制力及其行程输出基本相当。因此,本文设计的最优状态反馈保性能时滞补偿控制器能有效减小CSI效应的影响。

